Всего n=7+5=12 кроликов
По формуле классической вероятности
p=m/n=5/12 - вероятность вынуть черного кролика в одном испытании
q=7/12-вероятность вынуть белого кролика в одном испытании
Случайная величина Х – количество выбранных черных кроликов в четырех испытаниях
может принимать значения от 0 до 4
Х=0
означает, что ни разу не был выбран черный кролик.
Тогда вероятность этого события:
p₀=С⁰₄(5/12)⁰·(7/12)⁴
Х=1
означает, что один раз был выбран черный кролик.
Тогда вероятность этого события:
p₁=С¹₄(5/12)·(7/12)³
Х=2
означает, что два раза был выбран черный кролик.
Тогда вероятность этого события:
p₂=С²₄(5/12)²·(7/12)²
Х=3
означает, что три раза был выбран черный кролик.
Тогда вероятность этого события:
p₃=С³₄(5/12)³·(7/12)
Х=4
означает, что три раза был выбран черный кролик.
Тогда вероятность этого события:
p₄=С⁴₄(5/12)⁴·(7/12)⁰
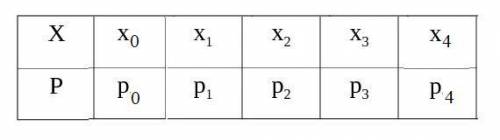
Закон распределения - таблица, в первой строке значения
Х от 0 до 4
во второй их вероятности.
заметим
1. x! (x > 4) оканчивается на 0 (x! = 1*2*...*(x-1)*x есть 2 и 5 в умножении)
2. квадраты чисел могут оканчиваться на цифры 0, 1, 4, 5, 6, 9
1! + 2! + 3! + 4! = 1 + 1*2 + 1*2*3 + 1*2*3*4 = 1 + 2 + 6 + 24 = 33
после 4-х решений нет
33 - не квадрат, далее числа, которые оканчиваются на 3, что тоже не может быть квадратом
Смотрим x=1, 2 , 3
1. x = 1
1 = y²
y = 1
y = -1
2. x = 2
1! + 2! = y²
y² = 3 нет решений в целых числах
3. х = 3
1! + 2! + 3! = y²
y² = 1 + 2 + 6 = 9
y = 3
y = -3
ответ (1,1) (1,-1) (3,3) (3,-3)