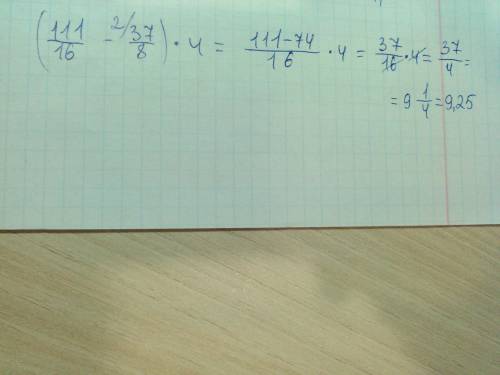
Найдем значение выражения (a ^ 2 - 1)/(5 * a ^ 2 + 5 * a) при а = - 2.
Для того, чтобы найти значение выражения (a ^ 2 - 1)/(5 * a ^ 2 + 5 * a), выражение сначала нужно упростить, а затем подставить известное значение в само выражение и вычислить его значение. То есть получаем:
(a ^ 2 - 1)/(5 * a ^ 2 + 5 * a) = (a - 1) * (a + 1)/(5 * a * (a + 1));
Числитель и знаменатель в дроби в правой части выражения сокращаем на (a + 1), тогда получим:
(a - 1) * (a + 1)/(5 * a * (a + 1)) = (a - 1) * 1/(5 * a * 1) = (a - 1)/(5 * a) = (- 2 - 1)/(5 * (- 2)) = (- 3)/(- 5 * 2) = - 3/(- 10) = 3/10.
Объяснение:
1) 25x + 50 = 0
25x = -50
x = -2
2) 7x + 15 = 0
7x = -15
x = -15 = - 2,14...
7
3) 10x - 4 = 0
10x = 4
x = 0,4
4) -3x + 15 = 0
-3x = -15
x = 5
5) -x -1 = 0
-x = 1
x = -1
6) -5x -12 = 32
-5x = 44
-x = 8,8
x = -8,8
7) -4x -2 = -19
-4x = -17
-x = -4,25
x = 4,25
8) 9x +4 = 8x
9x -8x = -4
x = -4
9) -x +9 = -4x
-x + 4x = -9
3x = -9
x = -3
10) - 7x +8 = 9x
-7x - 9x = -8
- 16x = -8
-x = -0,5
x = 0,5