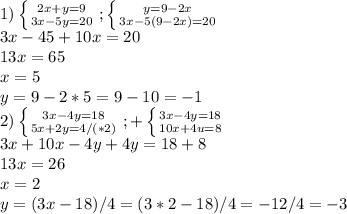
1/а.
Объяснение:
Преобразовать (упростить):
[(2a+3)/(2a-3)]*[(2a²+3a)/(4a²+12a+9)]-[(3a+2)/(2a+3)]+[(4a-1)/(2a-3)]-[(a-1)/a];
1)В скобках. Преобразовать:
числитель первой дроби:(2a²+3a)=а(2а+3);
знаменатель первой дроби:(4a²+12a+9)=(2а+3)²;
Вычитание:
[а(2а+3)/(2а+3)²] - [(3a+2)/(2a+3)]=
сокращение на (2а+3) в первой дроби:
=[а/(2а+3)] - [(3a+2)/(2a+3)]=
общий знаменатель (2a+3):
=(а-3а-2)/(2а+3)=
=(-2а-2)/(2а+3);
2)Умножение:
[(2a+3)/(2a-3)] * [(-2а-2)/(2а+3)]=
=[(2a+3)*(-2a-2)] / [(2а-3)*(2а+3)]=
сокращение на (2а+3) в числителе и знаменателе:
=(-2a-2)/(2а-3);
3)Сложение:
[(-2a-2)/(2а-3)] + [(4a-1)/(2a-3)]=
общий знаменатель (2а-3):
=(-2а-2+4а-1)/(2а-3)=
=(2а-3)/(2а-3)=1;
4)Вычитание:
1-[(а-1)/а]=
общий знаменатель а:
=(a-a+1)/a=
=1/a.
- 12 (минус четыре третьих)
Объяснение:
Первая дробь:
a*a - a - 6 = a * a + 2 * a - 3 * a - 6 = a * (a + 2) - 3(a + 2) = (a + 2) * (a - 3)
Отсюда сокращаем первую дробь и получаем: 1 / (a - 3).
Вторая дробь:
a * a - 6 * a + 9 = (a) ^ 2 - 2 * 3 * a + (3) ^ 3 = (a - 3) ^ 2 по формуле сокр. умножения.
1 / (a - 3) - a / (a - 3) ^ 2 = (a - 3) / (a - 3) ^ 2 - a / (a - 3) ^ 2 = -3 / (a - 3) ^ 2 - сложили дроби.
-3 / (a - 3) ^ 2 / (1 / (2a - 6) ^ 2) = -3 / (a - 3) ^ 2 * 4(a - 3) ^ 2. Сокращая (a - 3) ^ 2, получим - 12 (минус четыре третьих)
3x-5(9-2x)=20.
3x-45+10x=20
13x-45=20
13x=75
X=5
Y=9-10
x=5
Y=-1