Запишем эту сумму для произвольного числа слагаемых:
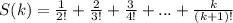
Вычислим значения S(k) для нескольких значений k:
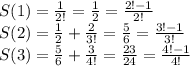
Тогда можно предположить, что
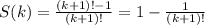
Но это ещё надо доказать. Используем индукцию. Выше было показано, что равенство верно для первых 3 натуральных k. Докажем, что из справедливости равенства для k=n следует справедливость равенства для k=n+1, тогда равенство можно будет считать справедливым для всех натуральных k.
Итак, предположим, что справедливо равенство
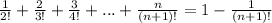
Проверим, верно ли, что
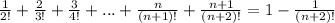
Подставляем сюда предыдущее выражение:
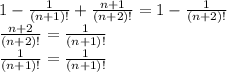
Получили верное равенство. Теперь можно вычислить значение нашей суммы:
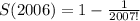
bn=b1•q^(n-1)=1/8•2^n:2=1/4•2^n
1/4•2^n=8
2^n=32
2^n=2^5
n=5
Является b5=8
1/4•2^n=12
2^n=48
Не является
1/4•2^n=16
2^n=64
2^n=2^6
n=6
Является b6=16
1/4•2^n=32
2^n=128
2^n=2^7
n=7
Является b7=32
ответ: вариант 2.
3. q=b2/b1=9/27=1/3
b6=b1•q^5=27•1/243=1/9
ответ: b6=1/9
4. 45–7n>0
–7n>–45
n<6 3/7
ответ: в последовательности 6 первых членов положительны, вариант 3.
5. a1=1400; d=100; an=5000; n-?
an = a1+d(n–1) = 1400+100n–100 =
= 1300+100n
1300+100n=5000
100n=3700
n=37
ответ: за 37 дней альпинисты покорили высоту.
6. {b1+b2+b3=112
{b4+b5+b6=14
{b1+b1•q+b1•q^2=112
{b1•q^3+b1•q^4+b1•q^5=14
{b1(1+q+q^2)=112
{b1•q^3(1+q+q^2)=14
Разделим первое уравнение на второе:
1/q^3=8
q^3=1/8
q^3=(1/2)^3
q=1/2
b1 = 112/(1+q+q^2) = 112/(1+1/2+1/4) =
= 112/(7/4) = (112•4)/7 = 64
b7=b1•q^6=64•1/64=1
ответ: b7=1