ответ: a=-25/36
Объяснение:
Исключим переменную z из системы уравнений.
Для этого умножим первое уравнение на (-3) :
-3x-3y-3z=-6x^2-9y^2
-x+2y+3z=a
Cложим уравнение 1 и 2:
-4x-y= a-6x^2-9y^2
6x^2-4x +9y^2-y=a
(√6x- √6/3)^2 +(3y-1/6)^2= a+2/3 +1/36= a + 25/36
(√6x- √6/3)^2 +(3y-1/6)^2=a+25/36
Когда : a+25/36 <0 решений нет , поскольку сумма двух квадратов число неотрицательное.
Когда : a+25/36=0 → a=-25/36
(√6x- √6/3)^2 +(3y-1/6)^2=0
В этом случае уравнение имеет единственное решение в силу того что квадраты неотрицательны.
√6x- √6/3=0
x=1/3
3y-1/6=0
y=1/18
z можно вычислить используя уравнение 2.
Если a+25/36>0
Значение x будет зависит от значения y.
Решение будет существовать при таких y когда:
(a+25/36)>(3y-1/6)^2
Таким образом решением данного уравнения будет совокупость двух отрезков, то есть решений будет больше чем одно.
Вывод: cистема уравнений имеет единственное решение , только когда a=-25/36
Рассмотрим неравенство:
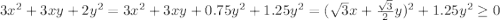
1. Если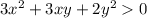 
, то оно будет равносильно неравенству
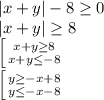
Рассмотрим уравнение:
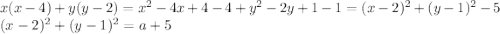
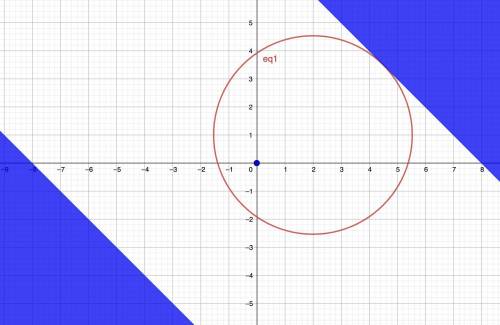
Это окружность с радиусом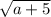 
и центром (2; 1). Изобразим это графически (см. рис. 1) Единственный случай, когда система имеет единственное решение, представлен на рисунке 1. При увеличении a окружность будет увеличиваться, и система будет иметь бесконечно много решений.
Радиус окружности перпендикулярен прямой y = -x + 8 и проходит через точку (2; 1). Значит, прямая, содержащая этот радиус, имеет вид y = x + m. Подставив x = 2, y = 1, получим m = -1. Найдём точку пересечения прямых y = x - 1 и y = -x + 8:
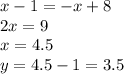
Это точка (4,5; 3,5), то есть центр некоторого квадрата. Заметим, что радиус равен 2,5 диагоналям квадрата со стороной 1. Значит,
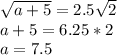
2. Если 
, то x = 0, y = 0. Тогда из уравнения следует, что a = 0. Тогда окружность будет иметь радиус 
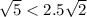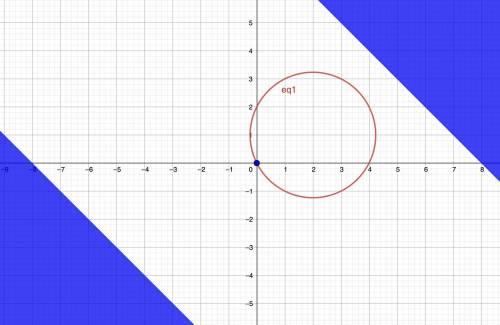
. Значит, с областью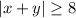 
она не будет иметь пересечений, и в данном случае решение единственно (рис. 2).
ответ: 0; 7,5
D=144-76=68
3(-6-√17)(-6+√17)+6+√17+6-√17=3(36-17)+12=69