Напомню, что значение обратной тригонометрической функции - это угол из какого -то промежутка, например, арксинус числа а, где IаI≤1
это угол из промежутка [-π/2; π/2] синус которого равен а. А как сравнить два угла? Больше тот, который больше.)
например, надо сравнить arcsin1/2 и arcsin0
Можно просто знать, что arcsin1/2=π/6, а arcsin0=0. Что больше? Разумеется, π/6.
Но можно сравнивать, прибегая к свойствам арксинуса. Т.к. у=sinх является кусочно-монотонной, строго возрастает на на отрезке [-π/2;π/2] и каждое свое значение на этом отрезке sinх достигает при единственном значении х, значит на этом отрезке существует функция у=arcsinх, которая тоже монотонно возрастает. Поэтому если у Вас есть значения аргумента арксинуса, и они не выходят за область определения, по значению аргументов можно сравнить и значения самих обратных тригонометрических функций. т.е. 1/2больше нуля, значит то arcsin1/2 больше arcsin0 , в силу возрастания арксинуса на указанном отрезке. Я показал это на примере арксинуса. Остальные аналогично сравнивают.
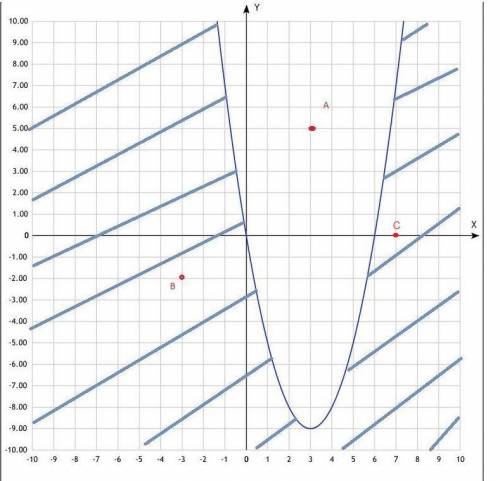
судя по заданию-график построен y=x^2-6x
решением неравенства
y<=x^2-6x- будет внешняя часть параболы, включая саму параболу. Если вы затрудняетесь с ее определением-совет: берите точку C (7;0) и подставляйте в неравенство
0<=49-42-верно. значит внешняя часть параболы, куда входит C (7;0)-решение. Сама парабола тоже решение- так как неравенство нестрогое. Область решения неравенства выделили штриховкой . как показано на чертеже.
По поводу точек А и В -поставлю их в плоскости рисунка.
А входит во внутреннюю область параболы-значит не является решением, В-во внешнюю, область штриховки, значит решение неравенства.
1) -7=-5•2=-10
2)-10-(-7)=-3
ответ: y=kx-b> -7=-5•2-(-3)