Составте уравнение по условию , обозначив буквой x количество яблок в первой карзине. в двух корзинах лежат яблоки, причём во второй корзине яблок в 3 раза больше, чем в первой. после того как в первую корзину добавили 6 кг яблок, а из второй взяли 2кг яблок, в обеих карзинах яблок стало поровну. сколько яблок было в первой корзине
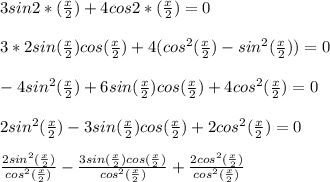 =0
=0
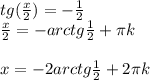 ,
,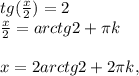
 k∈Z;
k∈Z;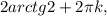 k∈Z.
k∈Z.
2 кор. 3х
х+6 - стало в 1 кор.
3х-2 - стало в 2 кор.
Уровнение
х+6=3х-2
-2х=-2-6
-2х=-8
х=8/2
х=4 было в 1 корзине