В решении.
Объяснение:
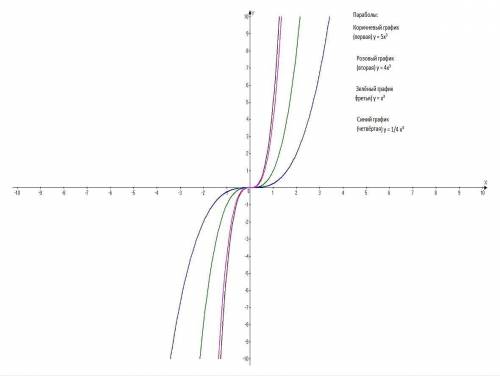
Построить в одной системе координат графики функций:
у = х³; у = 5х³; у = х³/4; у = 4х³.
Все графики - кубические параболы с вершиной в начале координат (0; 0). у = х³ - классическая парабола, остальные, в зависимости от коэффициента перед х³ "уже" или "шире" её.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
1) у = х³;
Таблица:
х -2 -1 0 1 2
у -8 -1 0 1 8
2) у = 5х³;
Таблица:
х -2 -1 0 1 2
у -40 -5 0 5 40
3) у = 1/4 х³ = х³/4;
Таблица:
х -3 -2 -1 0 1 2 3
у -6,75 -2 -0,25 0 0,25 2 6,75
4) у = 4х³;
Таблица:
х -2 -1 0 1 2
у -32 -4 0 4 32
Объяснение:
Варiанта х 0 1 2 3
Кратнiсть 4 3 2 1
Дисперсія Dₓ = X² - ( xₐ )² . Середнє арифм . досліджуваної ознаки
xₐ = ( 0*4 + 1*3 + 2*2 + 3*1 )/10 = 10/10 = 1 ; ( xₐ )² = 1² = 1 .
Середнє арифм . квадратів досліджуваної ознаки
Х² = ( 0² *4 + 1² *3 + 2² *2 + 3² *1 )/10 = 20/10 = 2 . Тоді шукане значення
дисперсії дорівнюватиме : Dₓ = 2 - 1² = 1 .
"Виправлена" дисперсія дорівнює :
s² = n/( n - 1 ) *Dₓ = 10/9 * 1 ≈ 1,11 .
Середнє квадратичне відхилення σₓ = √ Dₓ = √ 1 = 1 .
" Виправлене " середнє квадратичне відхилення
s = √ ( s² ) = √1,11 ≈ 1,05 .
4x²-6x+6x-9=4x²+4x-1
4x=-8
x=-2