Поступим следующим образом: косинус перенесем влево с противоположным знаком и обе части разделим на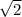 
(это же самое, что умножить на дробь 
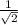) Имеем:
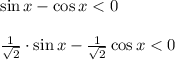
Заметим, что
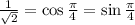
Если переписать неравенство в следующем виде -
,
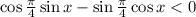то легко можно заметить в левой части формулу синуса разности аргументов. Окончательно имеем:
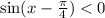
Сделаем замену: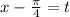 
. Таким образом мы свели исходное неравенство к наипростейшему вида 
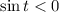. Решим его при числовой окружности (вложение). Окончательно имеем: 
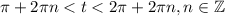. Возвращаемся к обратной замене: 
.
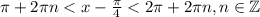Ко всем 3-ем частям неравенства прибавляем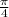 
и получаем окончательный ответ: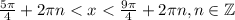 
ОТВЕТ: .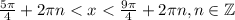
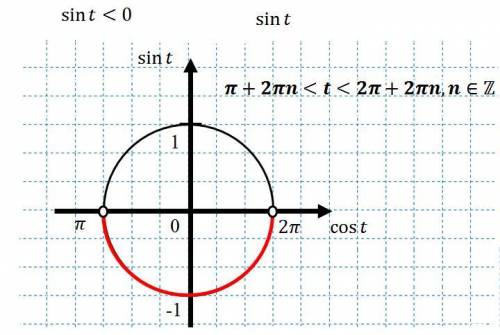
Eсли cosx > 0, т. е х в 1 и 4 четверти, делим на cosx
tgx < 1⇒ -(π/2)+πk < x < (π/4)+πk, k∈Z
Неравенству удовлетворяют корни, для которых соsx>0
Получаем
-(π/2)+2·πk < x < (π/4)+2·πk, k∈Z
Eсли cosx < 0, т. е х в 2 и 3 четверти, делим на cosx
tgx > 1⇒ (π/4)+πn < x < (π/2)+πn, n∈Z
Неравенству удовлетворяю корни, для которых соsx>0
Получаем
(3π/4)+2·πn < x < (π/2)+2·πn, n∈Z
О т в е т. Объединение ответов:
((π/2)+2·πk ; (π/4)+2·πk) U (3π/4)+2·πn ; (π/2)+2·πn), k, n∈Z
2t^2-t-1=0
a=2
b=-1
c=-1
D=b^2-4ac=9
t1,2=1+-3/4
t1=4/4
t2=1/2
син икс=1
x=pi/2+2pn, n принадлежит Z
sinx=1/2
x=(-1)^n pi/6+pin, n принад Z
x=(-1)^n 5pi/6 +pin, n принад Z