Дана функция y = x² + 2 + 6x
Перепишем ее в более удобном виде:
y = x² + 6x + 2
1. Для квадратного уравнения воспользуемся шаблоном:
ax² + bx + c = 0
Найдем коэффициенты:
a = 1;
b = 6;
c = 2;
2. Определим вершины по заданной формуле:

Подставим значения, найденные в пункте:
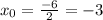
Подставим в изначальную формулу и найдём координату y вершины:
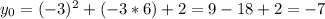
Запишем полученные данные
(-3; -7);
3.
Подставим значения в формулу:
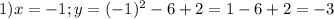
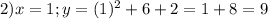
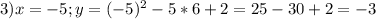

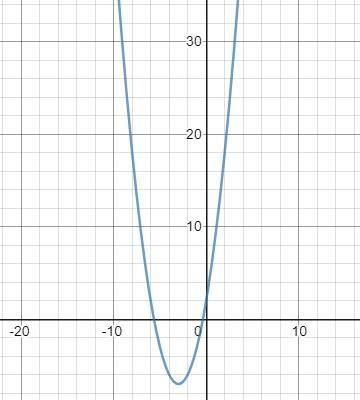
4. (График в прикрепленном файле)
5. Подставим значения:
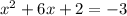
Перенесем "-3":
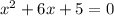
Решим квадратное уравнение:
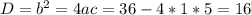
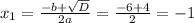
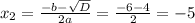
6. По графику функции видно, что наибольшее значение на этом значении при x = 0, а наименьшее это вершина:
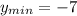
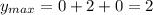
7. С обозначения параболы выплывает, что участок возрастания это все после вершины, а участок убывания до. Тогда:
Возрастания : (-3; +∞)
Убывания: (-∞; -3)
a*(-1)^2+b*(-1)+1=3 a-b+1=3 a-b=2
a*2^2+b*2+1=7 4*a+2*b+1=7 4*a+2*b=6
Из первого уравнения выделим а=2+в и подставим во второе уравнение
4*(2+в)+2*в=6 8+4*в+2*в=6 6*в=-2 в=-1/3 а=2+(-1/3)=5/3
Уравнение имеет вид y=(5/3)*x^2-(1/3)*x+1