При имеющихся исходных данным возможно 2 ответа:
1) b₁ = 6; q = 1/4;
1) b₁ = -6; q = -1/4;
Объяснение:
Член геометрической прогрессии с номером n вычисляется по формуле
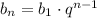
b₄ - b₂ = b₁ · q³ - b₁· q = b₁q(q² - 1)
b₆ - b₄ = b₁ · q⁵ - b₁· q³ = b₁q³(q² - 1)
По условию
b₁q(q² - 1) = -45/32 (1)
b₁q³(q² - 1) = -45/512 (2)
Преобразуем выражение (2)
b₁q³(q² - 1) = b₁q(q² - 1) · q²
В численном виде это можно записать как
-45/512 = -45/32 · q²
Откуда
q² = -45/512 : (-45/32)
q² = 1/16
q = ±1/4
Подставим q = 1/4 в выражение (1)
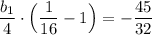
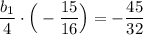
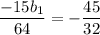
0.5b₁ = 3
b₁ = 6
Подставим q = -1/4 в выражение (1)
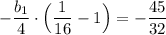
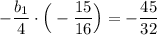

0.5b₁ = -3
b₁ = -6
Проверка:
1) b₁ = 6; q = 1/4
b₂ = 6 · 1/4 = 3/2
b₄ = 6 · 1/64 = 3/32
b₄ - b₂ = 3/32 - 3/2 = -45/32
b₆ = 6 · 1/1024 = 3/512
b₆ - b₄ = 3/512 - 3/32 = -45/512
2) b₁ = -6; q = -1/4
b₂ = -6 · (-1/4) = 3/2
b₄ = -6 · (-1/64) = 3/32
b₄ - b₂ = 3/32 - 3/2 = -45/32
b₆ = -6 · (-1/1024) = 3/512
b₆ - b₄ = 3/512 - 3/32 = -45/512
---.---.---.---.---.---.
Найдите при каком значении параметра p графики функций
1. f(x)=psin^2x+2cosx-p
2. g(x)=4-2pcosx
Имеют хотя бы одну общую точку
графики функций f(x) и g(x) имеют хотя бы одну общую точку означает
(аналитически ) что уравнение f(x)= g(x) имеет хотя бы одно решение.
psin²x+2cosx - p = 4 -2pcosx ; * * * sin²x+cos²x =1⇒sin²x =1 - cos²x * * *
р(1 -cos²x) + 2cosx - p = 4 -2pcosx ;
p*cos²x -2(p+1)*cosx +4 = 0 ;
Если p =0 (не квадратное уравнение) то получается уравнение cosx =2 которое не имеет решения. Значит должен быть ( p ≠ 0) квадратное уравнение.
Замена t =cosx , -1 ≤ t ≤1 * * * t∈ [ -1 ;1] * * *
уравнение принимает вид:
pt² -2(p+1)t² +4 = 0 ; D/4 =(p+1)² - 4 =(p-1)² ≥0 означает, что квадратное уравнение при всех значениях p имеет решения
t₁ =( p+1 +p -1 ) /p =2 ∉ [ -1 ;1] _ не решение
t₂ =( p+1 -(p -1) ) /p =2/p * * * р =1⇒ t₂=cosx =2 не имеет решение * * *
Первоначальное уравнение будет иметь решение ,если -1≤ t₂ ≤1
-1 ≤ 2/p ≤1 это двойное неравенство равносильно (⇔) системе неравенств: { 2/p ≥ -1≥0 ; 2/p ≤ 1. ⇔ { 2/p +1≥0 ; 1 -2/p ≥0. ⇔
{ (p+2)/p ≥0 ; (p-2)/p ≥0.⇒(методом интервалов ) p ∈ ( -∞ ; - 2] ∪ [ 2 ;∞) .
[-2] (0)
(0)[ 2]
ответ : p ∈ ( -∞ ; - 2] ∪ [ 2 ;∞) .