Дан многочлен -2x^4 - 23x^3 + 23x^2 + 55x +44 ≤ 0
Так как заданный многочлен имеет чётную высшую степень, то он имеет один и тот же предел при стремлении к плюс и к минус бесконечности.
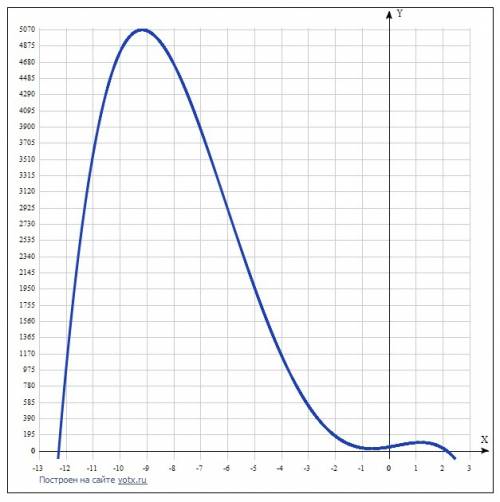
Если коэффициент при x^4 a<0, то функция убывает до минус бесконечности с обеих сторон, таким образом, функция имеет глобальный максимум.
Для решения заданного неравенства надо определить граничные точки, в которых график пересекает ось Ох.
То есть надо решить уравнение -2x^4 - 23x^3 + 23x^2 + 55x +44 = 0
Решения таких уравнений довольно сложные:
1 Через резольвенту
2 Решение Декарта — Эйлера
3 Решение Феррари.
Поэтому из четырёх корней этого уравнения приводим 2 действительных: х = -12,2667 и х = 2,13866.
С учётом приведенных выше рассуждений даём ответ:
х ≤ -12,2667 и х ≥ 2,13866.
х² = 5,7
х = √5,7
2) 5х² + 8х - 4 = 0
D = 8² - 4 * 5 * (- 4) = 144
х₁ = (- 8 + √144) : 10 = 0,4
х₂ = (- 8 - √144) : 10 = - 2
3) 9 (х - 2) - 3 (2х + 1) > 5х
9х - 18 - 6х - 3 > 5х
3х - 5х > 3 + 18
- 2х > 21
х < - 10,5
ответ: (- ∞; - 10,5)
4) {15 - x < 14,
4 - 2x < 5;
{15 - 14 < x,
4 - 5 < 2x;
{1 < x,
- 1 < 2x;
{x > 1,
- 0,5 < x;
{x > 1,
x > - 0,5.
ответ: (1; + ∞).