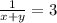- первая и вторая бригады работая вместе выполняют работу за 3 часа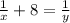
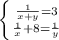
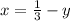
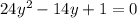
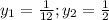
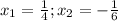
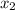не удовлетворяет условию, что x>0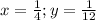
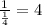часа
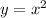- это парабола, с вершиной в точке (0;0). Она симметрична относительно оси OY. Ветви направлены вверх. Проходит через точки (0;0), (2;4), (-2;4)
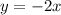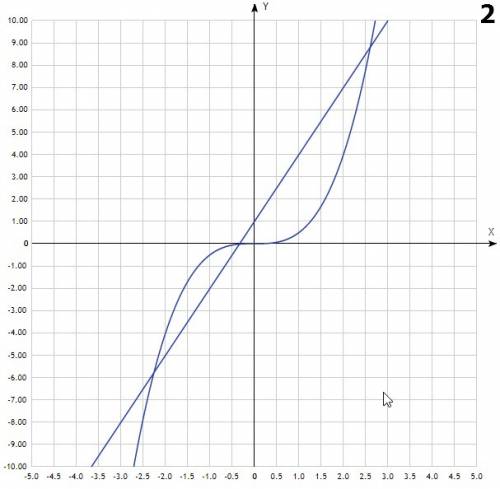
- это прямая, для её построения достаточно 2х точек. Например (0;0) и (-2;4)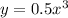
- кубическая парабола. График симметричен относительно начала координат, т.е. точки (0;0). 
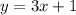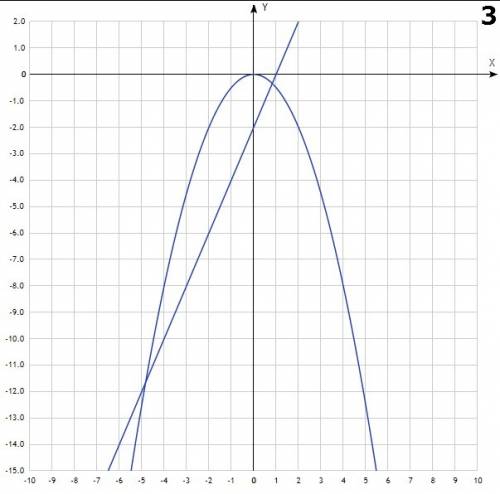
- прямая, проходящая через точки (0;1), (1;4)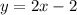
- прямая, проходящая через точки (0;-2) и (1;0)
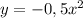- парабола, с вершиной в точке (0;0), симметричная относительно OY. Ветви направлены вниз.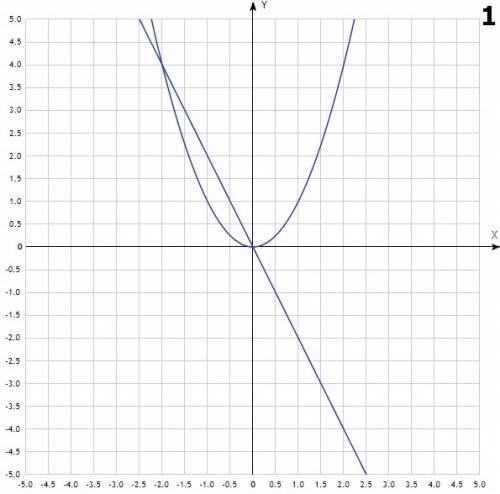 
y-f(x₀)=f`(x₀)·(x-x₀)
f(x₀)=f(π/2)=(1/2)sin(2·π/2)-2·(π/2)=(1/2)·(sinπ)-π=(1/2)·0-π=-π
f`(x)=(1/2)·(cos2x)·(2x)`=cos2x
f`(x₀)=f`(π/2)=cos(2·(π/2))=cosπ=-1
y-(-π)=-1·(x-(π/2))
y=-x-(π/2)