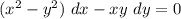

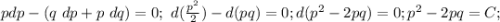
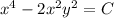
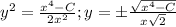
1) {3x - y = 3 Из первого ур-я вычтем второе
{3x -2y = 0
Получим у = 3, подставим это значение в 1 ур-е и найдем Х.
3х - 3 = 3 3х = 6 х = 2
ответ. (2; 3)
3) V(a^2 + b^2) при а = 12 и в = -5
V(12^2 + (-5)^2) = V(144 + 25) = V169 = 13
№2. в) x^2 + 4 < 0 не имеет решений т. к. x^2 >= при любом Х
и х^2 + 4 > 0 при любом Х.
1) {3x - y = 3 Из первого ур-я вычтем второе
{3x -2y = 0
Получим у = 3, подставим это значение в 1 ур-е и найдем Х.
3х - 3 = 3 3х = 6 х = 2
ответ. (2; 3)
3) V(a^2 + b^2) при а = 12 и в = -5
V(12^2 + (-5)^2) = V(144 + 25) = V169 = 13
№2. в) x^2 + 4 < 0 не имеет решений т. к. x^2 >= при любом Х
и х^2 + 4 > 0 при любом Х.
Убедимся, что данное дифференциальное уравнение является однородным. Воспользуемся условием однородности
Итак, дифференциальное уравнение является однородным.
Пусть
Получили уравнение с разделяющимися переменными
Интегрируя обе части уравнения, получаем
Обратная замена
Получили общее решение.