Question

Решить пример. (2p - 1)x² - (4p + 3)x + 2p + 3 = 0 при каких значениях параметра p уравнение имеет корни

Answer 1

Похожее задание было уже вчера или позавчера здесь. Ну да ладно)))
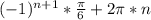
Суть в том, что есть на свете волшебная такая штука - дискриминант. (Похоже на слово дискриминация, правда?) Ну, он и производит дискриминацию - разделяет квадратные уравнения на те, где нет корней (это когда D<0); те, где корень всего один (когда D=0) и те, где корней два (D>0). Поэтому мы сейчас запишем выражение для нахождения дискриминанта (D=b^2-4ac), подставив а=2р-1; b=-(4p+3)= -4-3; c=2p+3, потом упростим его и посмотрим, при каких р он неотрицателен, а значит, уравнение имеет корни.
Итак, к делу:
$D=(-4p-3)^2-4*(2p-1)(2p+3)= \\ =16p^2+24p+9-4(4p^2-2p+6p-3)= \\ =16p^2+24p+9-16p^2+8p-24p+12= 8p+21 \\ \\ 8p+21 \geq 0 \\ 8p \geq -21 \\ p \geq -21:8 \\ p \geq -2,625$

ответ: х∈[-2,625; +∞).

(К слову: при р=0,625 решение уравнения будет одно, при p>0,625 их будет два.)