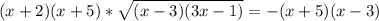

найдем дискриминант квадратного уравнения:
d = b² - 4ac = (-16)² - 4·1·48 = 256 - 192 = 64
так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
х₁ = 4, х₂ = 12
12² + (12-7)² = 13² - проверяем
144 + 25 = 169 и 13² = 169 13 больше 12 на 1, а 12 больше 5 на 7
3x²-10x+3≥0
D=100-36=84
x1=(10-8)/6=1/3 U x2=(10+8)/6=3
x≤1/3 U x≥3
x∈(-∞;1/3] U [3;∞)
x²+7x+10=(x+2)(x+5)
x1+x2=-7 U x1*x2=10⇒x1=-2 U x2=-5
15-2x-x²=(x+5)(3-x)
-(x²+2x-15)=0
x1+x2=-2 U x1*x2=-15⇒x1=-5 U x2=3
(x+2)(x+5)√(3x²-10x+3)=(x+5)(3-x)
(x+5)((x+2)√(3x²-10x+3)-(3-x))=0
x+5=0⇒x=-5
√(3x²-10x+3)=(3-x)
Возведем в квадрат
(x+2)²(3x²-10x+3)=(3-x)²
(x+2)²(3x-1)(x-3)=(x-3)²
(x-3)((x+2)²(3x-1)-(x-3))=0
x-3=0⇒x=3
(x²+4x+4)(3x-1)-x+3)=0
3x³-x²+12x²-4x+12x-4-x+3=0
3x²+11x²+7x-1=0
(x+1)(3x²+8x-1)=0
x+1=0⇒x=-1
3x²+8x-1=0
D=64+12=76
x1=(-8-2√19)/6=(-4-√19)/3
x2=(-4+√19)/3∉ОДЗ
ответ х=-5;x=-1;x=3;x=(-4-√19)/3