1) Аналитический.
2) Рекуррентній.
3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...
4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.
5)
6)
7) Это арифметическая прогрессия.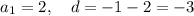 
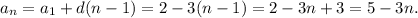
8)
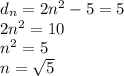
ответ: нет, не является, потому что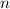 
должно быть натуральным числом.
9) 
Наибольшее натуральное 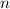, удовлетворяющее этому неравенству, — это 16.
ответ: 16 членов.
10)
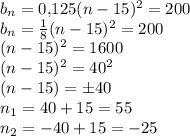
Второе решение не подходит, поскольку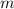 
должно быть натуральным числом.
ответ: 
a) x² + 3x - 130 = 0
D = 3² - 4 * 1 * (-130) = 9 + 520 = 529
x₁ = -3 + 23/2 = 20/2 = 10
x₂ = -3 - 23/2 = -26/2 = -13
б) x² - 2x + 10 = 0
D = (-2)² - 4 * 1 * 10 = 4 - 40 = -36
Дискриминант равен отрицательному числу. Уравнение не имеет решений.
в) x²- 6x + 34 = 0
D = (-6)² - 4 * 1 * 34 = 36 - 136 = -100
Дискриминант равен отрицательному числу. Уравнение не имеет решений.
г) 4x² - 4x = 3
4x² - 4x - 3 = 0
D = (-4)² - 4 * 4 * (-3) = 16 + 48 = 64
x₁ = 4 - 8/2 = -4/2 = -2
x₂ = 4 + 8/2 = 12/2 = 6
д) x²/2 - x/3 + 7*3/8 = 8
x²/2 - x/3 + 59/8 = 8 /*24
12x² - 8x + 177 = 192
12x² - 8x + 177 - 192 = 0
12x² - 8x - 15 = 0
D = (-8)² - 4 * 12 * (-15) = 64 + 720 = 784
x₁ = 8 - 24/24 = 16/24 = 2/3
x₂ = 8 + 24/24 = 32/24 = 4/3 = 1*1/3
е) x²/3 - 7x/18 + 4 = 5*1/9
x²/3 - 7x/18 + 4 = 46/9 / *18
6x² - 7x + 72 = 92
6x² - 7x + 72 - 92 = 0
6x² - 7x - 20 = 0
D = (-7)² - 4 * 6 * (-20) = 49 + 480 = 529
x₁ = 7 - 23/12 = -16/12 = -4/3 = -1*1/3
x₂ = 7 + 23/12 = 30/12 = 5/2 = 2*1/2
2)
побратски дай лучший ответ