12 яблок
Объяснение:
я думаю 12 потому что если суммарно 22 яблока, и на одной может быть 0, значит все 22 на оставшихся 5 яблонях. На всех яблонях разное число яблок. Что бы узнать. сколько может быть яблок максимально на яблоне, найдем вначале какое минимально возмоное число яблок может быть на яблоне. Очевидно что, 0 уже занят,тогда минимальное число будет 1 яблоко, на третьей яблоне 2, на четвертой 3. и на пятой яблоне минимально возможно 4 яблока. То есть на 5 яблонях суммарно минимально может быть 0+1+2+3+4=10 яблок. Тогда что бы получить 22 яблока на шести яблонях, на шестой яблоне должно быть 12 яблок. Это и есть максимальное число.
а)
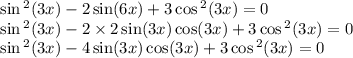
Проверим, может ли 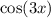 равняться нулю. Для этого подставим 0 в уравнение вместо косинуса:
равняться нулю. Для этого подставим 0 в уравнение вместо косинуса:
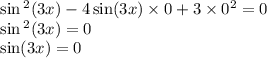
Получили, что при 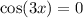 ,
, 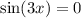 , но не бывает такого угла, косинус и синус которого одновременно обнуляются, поэтому
, но не бывает такого угла, косинус и синус которого одновременно обнуляются, поэтому 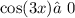 , следовательно мы можем разделить наше уравнение на косинус:
, следовательно мы можем разделить наше уравнение на косинус:
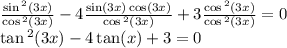
Получили квадратное уравнение относительно такнегса. За теоремой Виета находим корни данного уравнения:
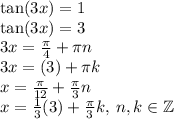
б) Необходимо отобрать корни уравнения на отрезке [-1;1]. Для этого воспользуемся двойным неравенством:
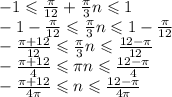
Для аппроксимации возьмём π ≈ 3:
![- \frac{3 + 12}{4 \times 3} \leqslant n \leqslant \frac{12 - 3}{4 \times 3} \\ - \frac{5}{4} \leqslant n \leqslant \frac{3}{4} \\n \in[ - 1.25;0.75]](/tpl/images/1717/4296/ee14b.png)
Учитывая, что n – целое число, на промежутке [-1;1], оно может принимать значения: -1, 0. Тогда корни на данном промежутке: 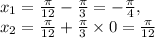 .
.
Отбираем второй корень по аналогии с первым:
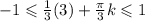
Мы знаем что функция arctg(x) довольно быстро изменяется в пределах от 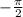 до
до 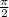 , поэтому для больших х
, поэтому для больших х 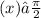 . Тогда
. Тогда
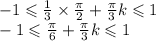
Сразу аппроксимируем π ≈ 3:
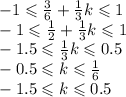
Для целых k в данный отрезок [-1;1] попадает только два значения k = -1 и k = 0. Тогда корни 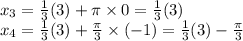 .
.
а) 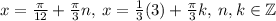 ;
;
б) 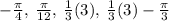 .
.
x> - 3
Объяснение:
x-1 x+3
x - x - 2 - 4 <2
x - 1 x+3
- 2 - 4 < 2
- 2 ( x - 1) - (x + 3) < 8
- 2x + 2 - x - 3 < 8
- 3x - 1 <8
- 3x < 8 +1
- 3 x < 9
x > - 3