Объяснение:
Как я понял, задача состоит в нахождении наибольшего значения функции. Для это необходимо найти производную этой функции и приравнять ее к 0 .
Правила взятия производной, необходимые для решения этого примера:
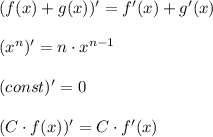
Эти правила можно описать следующим образом :
· Производная от суммы функций равна сумме их производных.
· Производная степенной функции равна произведению показателя степени на функцию, с показателем степени на 1 меньше исходного.
· Производная от постоянной величины равна 0.
· Постоянный множитель можно вынести за знак производной.
Тогда производная заданной функции равна :
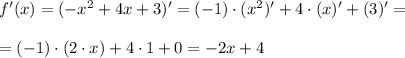
Приравняем производную к 0 и найдем корень уравнения:
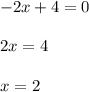
Подставим найденное значение в исходную функцию:
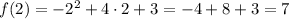
Получили, что наибольшее значение функции равно 7 в точке x=2
3x(a-b)-5y(b-a) = 3x(a-b)+5y(a-b) = (a-b)(3x+5y)
2y(n-m)+(m-n) = 2y(n-m)-(n-m) = (n-m)(2y-1)
(x+3)²-3(x+3) = (x+3)(x+3-3) = 3(x+3)
(x+3)(2y-1)-(x+3)(3y+2) = (x+3)(2y-1-3y-2) = (x+3)(-y-3)