ответ: 3 решения будет , когда a∈{49} ∪ {4*(10-√51)}
Объяснение:
Рассмотрим уравнение 1 :
(|y-10|+|x+3|-2)*(x^2+y^2-6)=0
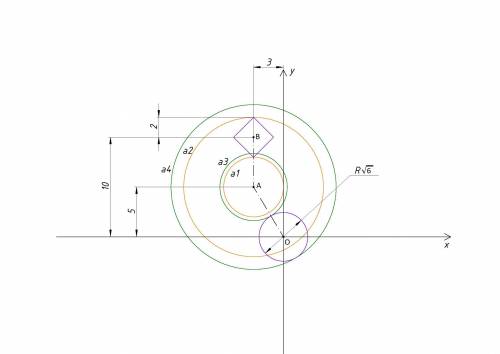
Уравнение представляет собой совокупность квадрата с центром в точке: B(-3;10) с половиной диагонали равной 2 и окружность с центром в начале координат и радиусом √6.
Рассмотрим уравнение 2
(x+3)^2+(y-5)^2=a -окружность с центром в точке : A (-3 ;5) и радиусом равным √a (находится на одной вертикали с квадратом из уравнения 1)
На рисунке показаны случаи касания окружности из уравнения к окружности и к квадрату из уравнения 1.
3 решения будет либо когда окружность из уравнения 2 касается квадрата (в 1 точке ) и пересекает окружность уравнения 1 ( в двух точках соответственно) , либо когда касается окружности уравнения и пересекает квадрат ( в двух точках соответственно).
Все обозначения смотрите на рисунке.
Найдем расстояния между центрами:
AB=10-5=5
AO=√(5^2+3^2)=√34
a1=5-2=3 → a=3^2=9
a2=5+2=7 → a=7^2=49
a3=√34-√6=√2* (√17-√3) → a= (√2* (√17-√3) )^2=40-4√51=4*(10-√51)
a4=√34+√6=√2*(√17+√3) → a= (√2*(√17+√3) )^2=4*(10+√51)
Cравним: a1 и a3
3 и √2* (√17-√3)
9 и 40-4*√51
4√51 и 31
816 < 961
Так же очевидно ,что :
a4=√34+√6 >√25+√4 =7=a2
a3=√34-√6<√49=7=a2
a4>a2>a3>a1
Тогда из рисунка видно, что 3 решения получается когда :
a=a3^2=4*(10-√51)
a= a2^2=49
a∈{49} ∪ {4*(10-√51)}
Теперь рассмотрим отдельно то , когда a=0
В этом случае уравнение 2 имеет вид :
(x+3)^2 +(y-5)^2=0
Поскольку квадрат число неотрицательное , то
x=-3 ; y=5
Но эта точка не принадлежит области первого уравнения.
ответ : 3 решения будет , когда a∈{49} ∪ {4*(10-√51)}
подставим 4а во второе уравнение системы. получим 4ху=2х²+2у²-2, упростим
-2ху+х²+у²=1; (х-у)²-1=0; (х-у-1)*(х-у+1)=0; 1)х=у+1 или 2)х=у-1 получили две прямые.
Если х=у+1,то 4у*(у+1)+2=а; 4у²+4у+2=а; (2у+1)²=а-1; Если а=1 ,то получим один корень, если а>1, то два корня. Если а<1, то корней нет.
Если рассмотреть первое уравнение, то при каждом a ≠ 0 — уравнение окружности c центром (0, 0) и радиусом а√2, тогда система при а=0 имеет единственное решение и поэтому не удовлетворяет условию задачи. При а≤0 уравнение не имеет смысла.
используем теперь результат выше и уточним ответ на задачу.
Если х=у+1, то у²+у²+2у+1=2а,у²+у+1/2=а; (у+1/2)²=а-1/4, при а=1/4 уравнение имеет одно решение, а при а >1/4 два различных решения.
Если х=у-1, то у²+у²-2у+1=2а,у²-у+1/2=а; (у-1/2)²=а-1/4, при а=1/4 уравнение имеет одно решение, а при а >1/4 два различных решения.
3(х - 2) - 5 = 2(3х + 1) - 1
3х + 3*(-2) - 5 = 2*3х + 2*1 - 1
3х - 6 - 5 = 6х + 2 - 1
3х - 11 = 6х + 1
3х - 6х = 1+11
-3х = 12
х= 12 : (-3)
х = - 4
=============================
3*(-4-2) -5=2*(3*(-4) +1) -1
3*(-6) -5 = 2*(- 11 ) - 1
-18 - 5 = - 22 - 1
- (18+5) = - (22+1)
- 23 = -23
2) у= ¹/₂ х + 4
- это линейная функция вида х=kx +b (прямая)
График строим по точкам :
х= -14 ⇒ у = ¹/₂ * (-14) + 4 = -7 +4 =-3
х = -8 ⇒ у= ¹/₂ * (-8) + 4 = -4 +4 = 0 (т. пересечения с осью ординат)
х = 0 ⇒ у = ¹/₂ * 0 + 4 = 0 +4 = 4 ( т. пересечения с осью абсцисс)
х = 8 ⇒ у= ¹/₂ * 8 + 4 = 4 + 4 = 8
график в приложении №1 .
у= 3 ⇒ ¹/₂ х + 4 = 3 ⇒ х = (3-4) : 0,5 ⇒ х = -2 (т. А)
№ 3 .
По условию Δ АВС - равнобедренный, следовательно:
1. боковые стороны равны : АВ=ВС
2. углы при основании АС равны :∠А = ∠С
3. ВL - биссектриса ∠В к основанию АС является медианой и высотой:
1) Биссектриса BL делит угол ∠В на две равные части :
∠АВL =∠CBL = ¹/₂ *∠B
2) Медиана BL - отрезок , соединяющий вершину с серединой противоположной стороны : АL = LC = ¹/₂ * AC
3) Высота BL - перпендикуляр из вершины В к стороне АС ⇒ ВL⊥AC
∠ВLA = ∠BLC = 90°
Рассмотрим ΔВLC :
1. ∠ВLC = 90° (п. 3.3)) ⇒ ΔBLC - прямоугольный
2. LD - биссектриса ∠ВLD :
∠ВLD = ∠DLC = ¹/₂ * ∠ BLC
∠BLD =∠DLC = ¹/₂ * 90° = ⁹⁰/₂ = 45°
Чертеж в приложении №2.
ответ: ∠BLD = 45°.