а) 1/2
б) 3
в) 2 целых и 6/11
г) 3/14
д) -6
Объяснение:
Степени с минусом можно представить, как обычные степени дробью в перевёрнутом виде. Например, 2=2/1, а 2^-1=1/2, тоже самое с примером б)
В примере в) 1/4+1/7 приводятся к общему знаменателю путём перемножения 4*7=28
У 1/4 числитель и знаменатель умножаются на 7=7/28
У 1/7 числитель и знаменатель умножаются на 4=4/28
Теперь их можно объединить и сложить (7+4)/28=11/28
1/(11/28)=28/11=2целых и 6/11
Аналогично предыдущим примерам:
(7^-1)+(14^-1)=1/7+1/14
Наименьший общий знаменатель здесь 14, то есть 7*2
У 1/7 числитель и знаменатель умножаются на 2
Складываем:(2+1)/14=3/14
Пример д)
Общий знаменатель здесь 6ас
6а/с умножаем числитель и знаменатель на 6а
(с-36а)/6а умножаем на с
Объединяем:
(36а^2-(36а^2+с^2)+(с^2-36ас))/6ас=(36а^2-36а^2-с^2+с^2-36ас)/6ас=-36ас/6ас=-6
Если перед скобками стоит знак "-", то все цифры в скобках при раскрытии идут с противоположным знаком.
Максимум в точке х =  (для записи
(для записи 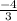 )
)
Минимум в точке х = -1
Объяснение:
f(x)=2x^3+7x^2+8x+4
Область определения:
Х∈R
f(x)=2x^3+7x^2+8x+4, Х∈R
Определим производную f:
f(x) = 2x^3+7x^2+8x+4
f'(x) = d/dx (2x^3+7x^2+8x+4)
f'(x) = d/dx(2x^3) + d/dx(7x^2) + d/dx(8x) + d/dx(4)
f'(x) = 2*3x^2 + 7*2x+8+0
f'(x) = 6x^2+14x+8
f'(x) = 6x^2+14x+8, Х∈R
Представим f'(x) = 0
0=6x^2+14x+8
Решим ур-е относительно Х
6x^2+14x+8=0 | :2
3x^2+7x+4=0
D=b2-4ac = 7^2-4*3*4 = 1
x1,2= -b+-D/2a = -7+-1/2*3
x1= - 4/3
х2= -1
X∈(-∞;- 4/3)
X∈(- 4/3;-1)
max: - 4/3
min: -1
при x∈(-∞,5/12) y'>0 ⇒ функция возрастает
при x∈(5/12,∞) y'<0 ⇒ функция убывает
таким образом в точке x=5/12 находится максимум