1) на путь по течению реки катер затратил 3 часа, а на обратный путь 4 часа. какова скорость течения реки, если собственная скорость катера 14 кмч 2) катер, имеющий собственную скорость 15 кмч, проплыл 2 часа по течению реки. на обратный путь он затратил 3 часа. какова скорость течения реки
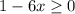 откуда
откуда 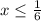 (почему так? Потому что подкоренное выражение должно принимать неотрицательное значение)
(почему так? Потому что подкоренное выражение должно принимать неотрицательное значение)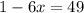

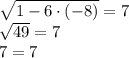
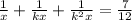 .
.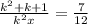 .
.
Пусть x км/ч-скорость течения реки,тогда
14-x км/ч-скорость против течения
14+x км/ч-скорость по течения
По условию задачи,путь туда и обратно одинаковый,значит
(14+x)×3=(14-x)×4
42+3x=56-4x
3x+4x=56-42
7x=14
x=14÷7
x=2 км/ч-скорость течения реки
2)
По такому же принципу что и первая задача
x км/ч-скорость течения реки
(15+x)×2=(15-x)×3
30+2x=45-3x
2x+3x=45-30
5x=15
x=15÷5
x=3 км/ч-скорость течения реки