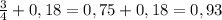
20 дней и 30 дней.
Объяснение:
Пусть один из сварщиков может выполнить всю работу за х дней,
тогда другой сварщик - за (25 * 2 - х) дней или (50 - х) дней.
Примем всю работу за 1, тогда производительность труда у первого сварщика равна 1/х, у второго сварщика - 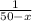 .
.
Совместна производительность труда двух сварщиков равна:
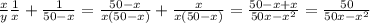
Составим уравнение и решим его:
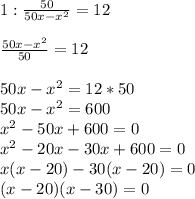
1) x - 20 = 0
x = 20 (дней)
2) x - 30 = 0
x = 30 (дней)
Допустим, что один из сварщиков может выполнить всю работу за 20 дней, тогда второй сварщик может выполнить всю работу за:
50 - 20 = 30 (дней) и наоборот.
1) Найдем первые члены последовательности
b(1)=1^2-4=-3
b(2)=2^2-4=0
b(3)=3^2-4=5
b(4)=4^2-4=12
b(5)=5^2-4=21
последовательность возроастающая, значит следующие члены будут большими за 21
значит нам подходят только -3, 0, 21
можно было иначе -3=n^2-4 откуда натуральное n равно 1
6=n^2-4 такого натурального n нет
0=n^2-4 откуда натуральное n равно 2
21=n^2-4 откуда натуральное n равно 5
второй вариант поиска более верный, но у нас небольшие числа можно искать и по первому)
2) знаменатель равен b2\b1 или b3\b2 и так далее ,то есть отношению следующего члена прогрессии к предыдущему
b1=3 b2=1 b3=1\3 ...
значит он равен 1\3
ответ г)1/3
3) ищем знаменатель 1\3 : 1\6 =2 q=b2\b1
значит х =1\3 *2=2\3 b3=b2*q
ответ: 2\3