y наиб = у max = 54
Объяснение:
Дана функция y= (27 - x) · √x
Производная этой функции 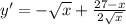
Упростим это выражение 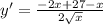
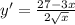
х ≠ 0 , но этот разрыв производной нас не интересует, поскольку мы ищем наибольшее значение в интервале [1; 16]
y' = 0
(27 - 3x) = 0
Точка экстремума одна x = 9.
При х < 9 y' > 0; при х > 9 y' < 0. Следовательно, точка х = 9 - точка максимума. И на концах интервала при непрерывной производной в заданном интервале значения функции будут меньше её значения в точке локального максимума.
у наиб = у max = y(9) = (27 - 9) · √ 9 = 54
у'=2е^х+2хе^х
2е^х (1+х) =0
х=-1
е^х никогда не равно 0 ни при каких х
следовательно на оси х наносим точку -1, на промежутке от -бесконечность до -1 производная имеет знак минус (функция убывает) , на промежутке от -1 до +бесконечности производная имеет знак плюс (функция возрастает)