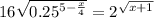
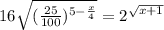
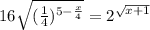
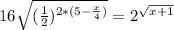
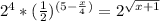
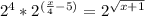
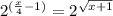
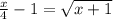
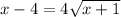

Легко побачити, що кожне число збільшується на 5 тому задаємо арифметичну прогресію з першим членом – 1 і різницею – 5:
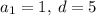
Оскільки ми не знаємо порядковий номер х-а, запишемо йому номер n:
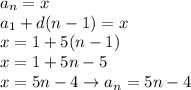
У рівнянні маємо суму чисел послідовності.
Загальна формула суми арифметичної прогресії:

Підставимо у формулу відомі нам складові:
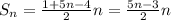
За умовою дана сума дорівнює 342, тоді:
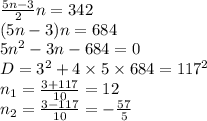
Оскільки n – порядковий номер члена прогресії, він не може бути від'ємний тому n ≠ -57/5 => n = 12.
Так як ми знаємо n, ми можемо знайти x:

Відповідь: 56
1)
Основание АD трапеции ABCD лежит в плоскости α .Через точки B и C проведены параллельные прямые , пересекающие плоскость α в точках E и F соответственно.
1) Каково взаимное расположение прямых EF и AB?
(Уточняем - в плоскости α лежит только АД, а ВС - не лежит. В противном случае ВЕ и СF не пересекали бы плоскость α, а лежали в ней).
ВС параллельна АD ⇒ параллельна плоскости α.
АD параллельна ВС, ЕF параллельна ВС. Две прямые , параллельные третьей прямой, параллельны.
⇒ ЕF параллельна АD и параллельна плоскости АВСD, но не параллельна АВ, которая пересекается с АD.
⇒ Прямые EF и AB - скрещивающиеся.
2) Чему равен угол между прямыми EF и AB, если ABC = 150°?
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
Сумма углов при боковой стороне трапеции 180°, следовательно, угол ВАD=180°-150°=30°.
Проведем в плоскости ВЕF прямую ЕК, параллельную АВ.
ЕК|║АВ; ЕF║АD Углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.⇒
∠FЕК=∠ВАD=30°
ВЕ и СF могут быть проведены в плоскости АВСD.
Тогда ЕD будет лежать на АD и в этом случае непараллельные прямые EF и АВ лежат в одной плоскости. Тогда АВ и EF пересекyтся.
2) 1.Каково взаимное расположение прямых PK и AB? - скрещиваются, РК параллельна АС, как средняя линия, значит она не пересекает АС, а значит не имеет общих точек с плоскостью АВС.
2.Чему равен угол между прямыми PK и AB, если ABC = 40° и BCA = 80°?
PK и AB скрещиваются, так как они не параллельны и не пересекаются. Искомый угол
равен углу BAC.
Угол BAC = 180 - 40 - 80 = 60.
Объяснение:
16=2^4
2^4*2^(x/4-5)=2^√(x+1)
2^(4+x/4-5)=2^√(x+1)
2^(x/4-1)=2^√(x+1)
x/4 -1=√(x+1)
ОДЗ
{x/4-1≥0⇒x/4≥1⇒x≥4
{x+1≥0⇒x≥-1
x∈[4;∞)
домножим на 4 и возведем в квадрат
x-4=4√(x+1)
x²-8x+16=16x+16
x²-24x=0
x*(x-24)=0
x=0∉ОДЗ
x=24