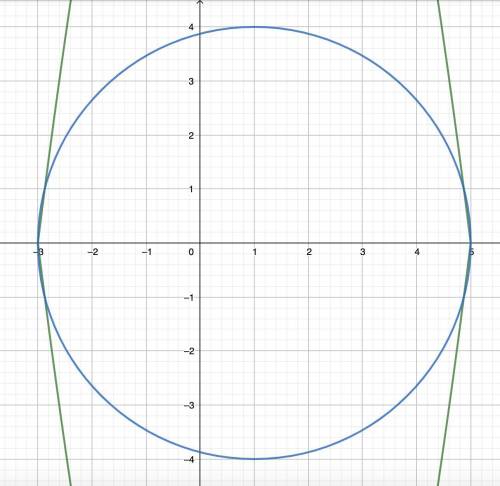
![\left \{ {{2^{x}+3\cdot 2^{-x} \leq 4} \atop { \frac{2x^2-8x}{x-7}\leq x }} \right. \\\\1)\; \; 2^{x}+\frac{3}{2^{x}}-4 \leq 0\; ,\; \; t=2^{x}\ \textgreater \ 0\\\\t+ \frac{3}{t} -4 \leq 0\; ,\; \; \frac{t^2-4t+3}{t} \leq 0\; ,\; \; \frac{(t-1)(t-3)}{t} \leq 0\\\\Znaki:\; \; \; ---(0)+++[\, 1\, ] ---[\, 3\, ]+++\\\\t\in (-\infty ,0)\cup [\, 1,3\, ]\\\\t\ \textgreater \ 0\; \; \Rightarrow \; \; 1 \leq 2^{x} \leq 3\; \; \Rightarrow \; \; 0 \leq x \leq log_23](/tpl/images/0774/4515/6afd6.png)
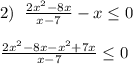
![\frac{x^2-x}{x-7} \leq 0\; ,\; \; \; \frac{x(x-1)}{x-7} \leq 0\\\\Znaki:\; \; \; ---[\, 0\, ]+++[\, 1\, ]---(7)+++\\\\x\in (-\infty ,0\, ]\cup [\, 1,7)\\\\3)\; \; \; 1\ \textless \ log_23\ \textless \ 7\; \; \Rightarrow \; \; \; x\in [\, 1,\, log_23\, ]\; \; -\; \; otvet](/tpl/images/0774/4515/4c398.png)
Рассмотрим первое уравнение:
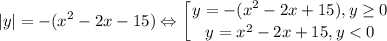
Данную совокупность можно представить в виде графика: начертим две параболы и оставим только их части выше (в первом случае) и ниже (во втором) оси абсцисс.
Рассмотрим второе уравнение:
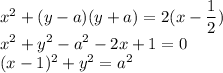
Оно задаёт окружность радиусом |a|.
Оба графика симметричны относительно прямых y = 0 и x = 1. Если окружность касается парабол внутренним образом, система имеет 4 решения, затем, если увеличивать радиус, при пересечении она имеет 8 решений. Когда окружность проходит через общие точки частей парабол (-3; 0), (5; 0), система имеет 6 решений. Затем при пересечении — 4 решения, при внешнем касании — 2 решения.
В случае, когда реализуется 6 решений, окружность проходит через точку (5; 0). Её центр расположен в точке (1; 0). Значит, радиус равен 4:
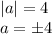
ответ: ±4