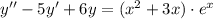
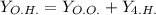
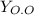

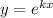 , тогда имеем характеристическое уравнение
, тогда имеем характеристическое уравнение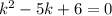
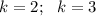
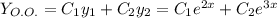
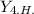 ( С1, С2 принимаем за функции)
( С1, С2 принимаем за функции)
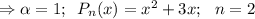
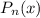 - многочлен степени х
- многочлен степени х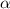 с корнями характеристического уравнения и принимая во внимания что n=2 частное решение будем искать в виде
с корнями характеристического уравнения и принимая во внимания что n=2 частное решение будем искать в виде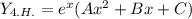
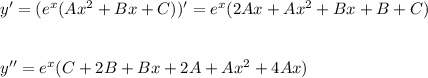
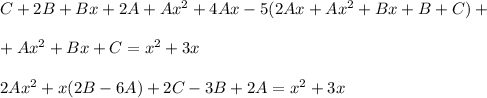
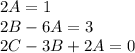
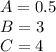
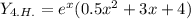
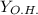
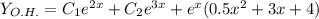 - ответ
- ответ
Объяснение:
Системы уравнений.
1) (x+2)²+y²=10; x²+4x+4+y²=10; x²+4x+y²=10-4; x²+4x+y²=6
x+y+4=0; y=-x-4
x²+4x+(-x-4)²=6
x²+4x+x²+8x+16=6
2x²+12x+10=0 |2
x²+6x+5=0; D=36-20=16
x₁=(-6-4)/2=-10/2=-5; y₁=5-4=1
x₂=(-6+4)/2=-2/2=-1; y₂=1-4=-3
ответ: (-5; 1); (-1; -3).
2) y+4x=6; y=6-4x
x²+3xy-y²=3; (x-y)(x+y)+3xy=3
(x-6+4x)(x+6-4x)+3x(6-4x)=3
(5x-6)(6-3x)+18x-12x²=3
30x-15x²-36+18x+18x-12x²-3=0
-27x²+66x-39=0 |(-1)
27x²-66x+39=0; D=4356-4212=144
x₁=(66-12)54=54/54=1; y₁=6-4·1=2
x₂=(66+12)/54=78/54=13/9=1 4/9; y₂=6 -4·13/9=6 -52/9=5 9/9-9 7/9=2/9
ответ: (1; 2); (1 4/9; 2/9).
Т.е. данное неравенство разбивается на пару случаев:
Так как нам нужны все решения. То получаем систему:
Ч.Т.Д.