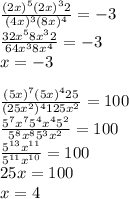
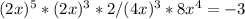
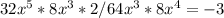
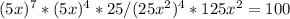
запись |х| <= 1 означает, что -1 <= x <= 1
(или другими словами ---эквивалентна двойному неравенству...)
значит для этих значений х нужно выбрать часть параболы (Вы ее правильно описали: из начала координат, ветви вниз): ветви параболы берем только до точек с абсциссами -1 и 1 (т.е. верхнюю часть параболы... от точки (-1; -1) до точки (1; -1))
аналогично для гиперболы...
|х| > 1 соответствует объединению двух интервалов: (-бесконечнось; -1) U (1; +бесконечнось)
из 3 квадранта возьмем только часть гиперболы,
соотв. интервалу на оси ОХ (-бесконечнось; -1) ---граница не входит... (т.к. |х| > 1)
из 1 квадранта возьмем часть гиперболы,
соотв. интервалу на оси ОХ (1; +бесконечнось) ---граница не входит... (т.к. |х| > 1)
(остальную часть гиперболы (или параболы) как-будто стираем...)
если нужно ---прикреплю рисунок...
А) 0,(31). Эта дробь являются чистой периодической десятичной дробью. Следовательно, имеем: 0,(31) = 31/99.
Б) 0,(013). Эта дробь также являются чистой периодической десятичной дробью. Следовательно, имеем: 0,(013) = 13/999.
В) 3,7(14). Сначала отделим целую часть: 3,7(14) = 3 + 0,7(14). Рассмотрим дробную часть по отдельности и применим к ней правило представления смешанной периодической дроби в виде обыкновенной дроби. Имеем: 0,7(14) = (714 – 7) / 990 = 707/990. Следовательно, 3,7(14) = 3 + 707/990 = 3707/990.
ответы: 0,(31) = 31/99; 0,(013) = 13/999; 3,7(14) = 3707/990.