2
.
Объяснение:
В ней найдем строку с нужной нам функцией, то есть косинусом, а среди значений функции найдем указанное в условии значение, то есть – корень из 2 / 2. Теперь мы можем определить значение одного из аргументов, при котором косинус будет равен – корень из 2 / 2. Таким значением является угол 3 Пи / 4 или 135 градусов.
Поскольку функция косинус является периодичной, то данное значение будет не единственным. Период функции косинус равен 2 Пи, следовательно, все возможные решения данного уравнения опишутся множеством решений:
х = 3 Пи / 4 + 2 Пи k, k принадлежит множеству целых чисел.Можно уравнение решить через обратную функцию к косинусу. В таком случае:
х = ± arccos (– корень из 2 / 2) + 2 Пи k.
По свойству арккосинуса:
x = ± (Пи – arccos (корень из 2 / 2)) + 2 Пи k
x = ± (Пи – (Пи / 4)) + 2 Пи k
x = ± (3 Пи / 4) + 2 Пи k.
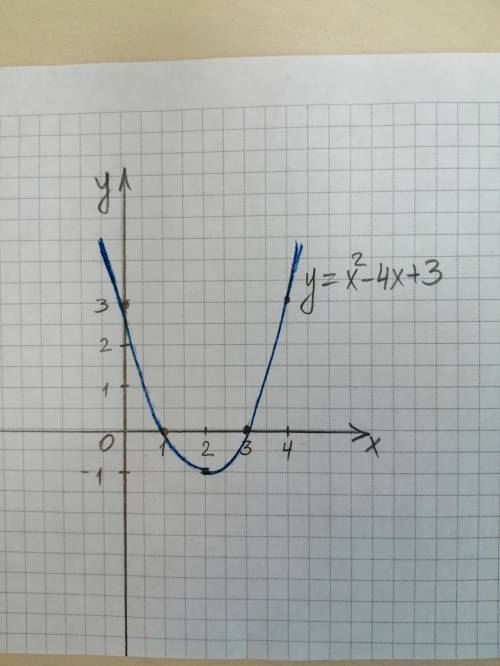
y=x²-4x+3
y=ax²+bx+c
a=1, b=-4, c=3
1) Координаты вершины параболы:
х(в)= -b/2a = -(-4)/(2*1)=4/2=2
у(в) = 2²-4*2+3=4-8+3=-1
V(2; -1) - вершина параболы
2) Ось симметрии параболы проходит через вершину параболы параллельно оси Оу, значит, ось симметрии можно задать уравнением х=2
3) Точки пересечения графика функции с осями координат:
с осью Оу: х=0, y(0)=0²-4*0+3=3
Значит, (0;3) - точка пересечения параболы с осью Оу
с осью Ох: у=0, x²-4x+3=0
D=(-4)²-4*3*1=16-12=4=2²
x₁=(4+2)/2=6/2=3
x₂=(4-2)/2=2/2=1
(3;0) и (1;0) - точки пересечения с осью Ох
4) Строим график функции:
Уже найдены вершина параболы и точки пересечения с осями координат. Точка (4;3) - расположена симметрично точке (0;3) относительно оси симметрии параболы
5) По рисунку видно, что график функции находится в I, II и IV четвертях.
Объяснение:
1) sin(π√x) = 1 и sin(π√(x+6)) = 1
Решением первого будет:
π√x = π/2 + 2πn, где n∈Z, или √x = 1/2 + 2n, или x = (2n + 1/2)²
Решением второго:
π√(x+6) = π/2 + 2πm, где m∈Z, или √(x+6) = 1/2 + 2m, или x = (2m +1/2)² - 6
Приравняем оба решения друг другу: (2n + 1/2)² = (2m + 1/2)² - 6
Перепишем: (2m + 1/2)² - (2n + 1/2)² = 6
По формуле разности квадратов:
(2m + 1/2 - 2n - 1/2)*(2m + 1/2 + 2n + 1/2) = 6
(2m - 2n)*(2m + 2n + 1) = 6
(m - n)*(2m + 2n + 1) = 3
Произведение равно простому числу, значит, сомножители м.б. равны (+1) и (+3) или (-1) и (-3). Однако из решений √x = 1/2 + 2n и √(x+6) = 1/2 + 2m следует, что n≥0 и m≥0. Отсюда (2m + 2n + 1) ≥ 1, а значит, и (m - n) ≥ 0. Поэтому рассмотрим только следующие два варианта.
а) m - n = 1; 2m + 2n + 1 = 3;
m - n = 1; m + n = 1;
Отсюда, m=1 и n =0. Тогда, x = (2*0 + 1/2)² = 1/4 и x = (2*1 +1/2)² - 6 = 1/4
Есть решение: x = 1/4, значение проходит проверку.
б) m - n = 3; 2m + 2n + 1 = 1;
m - n = 3; m + n = 0;
Отсюда, 2m = 3, решения нет, m - не целое число.
Итак, x = 1/4
2. sin(π√(x) = -1 и sin(π√(x+6) = -1;
Решением первого будет:
√x = 2n - 1/2; x = (2n - 1/2)^2
Решением второго:
√(x+6) = 2m - 1/2; x = (2m - 1/2)^2 - 6
Делаем всё аналогично.
(2n - 1/2)² = (2m - 1/2)² - 6; (2m - 1/2) ² - (2n - 1/2)² = 6;
(2m - 1/2 - 2n + 1/2)*(2m - 1/2 + 2n - 1/2) = 6
(2m - 2n)*(2m + 2n -1) = 6
(m - n)*(2m + 2n - 1) = 3
Произведение равно простому числу, значит, сомножители м.б. равны (+1) и (+3) или (-1) и (-3). Однако из решений √x = 2n - 1/2 и √(x+6) = 2m - 1/2 следует, что n≥1 и m≥1. Отсюда (2m + 2n + 1) ≥ 3, а значит, и (m - n) ≥ 0. Более того, (2m + 2n + 1) = 3 и (m - n) = 1. Этот вариант и рассмотрим.
m - n = 1; 2m + 2n - 1 = 3;
m - n = 1; m + n = 2;
Отсюда, 2m = 3, решения нет.
ответ: x = 1/4