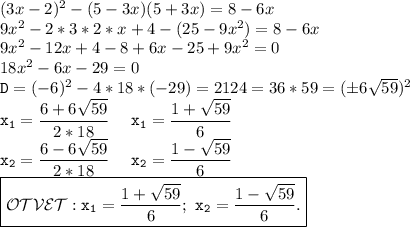
ответ: функция имеет максимум zmax=12 в точке M(4;4).
Объяснение:
1) Находим первые частные производные:
z'x=y/(2*√x)-1, z'y=√x-2*y+6
Приравнивая их к 0, получаем систему уравнений:
y/(2*√x)-1=0
√x-2*y+6=0
Решая её, находим x=4 и y=4 - координаты единственной критической (стационарной) точки M.
2) Находим вторые частные производные:
z"xx=-y/(4*√x³), z"xy=1/(2*√x), z"yy=-2
и вычисляем их значения в точке M:
A=z"xx(M)=-1/8, B=z"xy(M)=1/4, C=z"yy(M)=-2
3) Составляем выражение A*C-B² и находим его значение. Оно равно 3/16>0, поэтому функция z действительно имеет экстремум в точке М. И так как при этом A<0, то это - максимум. Его значение zmax=4*√4-4²-4+6*4=12.
Таких примеров можно привести много. Разберём один из них и принцип решения:
Пусть, например первые пять чисел равны 1, 2, 3, 4 и 5, а шестое число равно х (х≠0).
Тогда произведение этих чисел равно 1*2*3*4*5*х
Увеличим каждое из чисел на 1, получим числа: 2, 3, 4, 5, 6 и х+1.
Их произведение равно 2*3*4*5*6*(х+1).
По условию, от увеличения каждого из чисел на единицу, их произведение чисел не изменилось. Составим уравнение:
1*2*3*4*5*х = 2*3*4*5*6*(х+1)
х = 6(х+1)
х = 6х+6
х-6х = 6
-5х = 6
х = -6:5
х = -1,2
1, 2, 3, 4, 5, -1,2
используем (a-b)²=a²-2ab+b² (a²-b²)=(a-b)(a+b)
9x² - 12x + 4 - (25 - 9x²) - 8 + 6x =0
9x² + 9x² - 12x + 6x +4 - 25 - 8 =0
18x² - 6x - 29 = 0
если есть квадратное уравнение ax²+bx+c=0 то корни уравнения можно найти через дискриминант D=b²-4ac x₁₂=(-b+-√D)/2a
D= 36 + 4*18*29 = 2124
x₁₂=(6+-√2124)/36 =(6+-6√59)/36 = (1+-√59)/6