Объяснение:
здесь надо рассмотреть два случая
1) х-5>0, x>5, тогда |x-5|=x-5 и 1/(х-5) -2<0, (1-2x+10)/(x-5) <0,
(11-2x)/(x-5) <0 , - __(5)+___(5,5)___-___
общее решение x>5,5 (с учетом, что x-5>0)
2) x-5<0, x<5, тогда |x-5|=5-x и получим уравнение:
1/(5-x) -2<0, (1-10+2x)/ (5-x) <0, (2x-9)/ (5-x) <0
-___(4,5)+(5)___- и общее решение
x<4,5 (с учетом, что x-5<0) , объединяем два случая и
ответ: (-Б; 4,5) и (5,5; +Б) (Б- бесконечность)
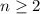равных частей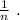
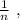нужно разрезать верёвочку длины 2 на 
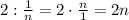частей.
частей.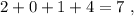
не делится на три.
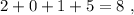не делится на три.
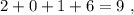делится на три!
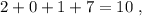не делится на три.
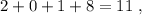не делится на три.
AC^2 = AB^2 + BC^2 - 2*AB*BC*cos(B)
По значению синуса угла В найдём косинус этого угла, используя основное тригонометрическое тождество:
sin^2(B) + cos^(B) = 1;
cos^2(B) = 1- sin^2(B) = 1- ((√19)/10)^2 = 1 - 19/100 = 81/100 или
cos(B) = 9/10
В формулу теоремы уосинусов подставляем значения:
6^2 = AB^2 + 6^2 - 2*AB*6*(9/10);
Упрощаем и сокращаем на AB:
0 = AB^2 - 54*AB/5; AB^2 = 54*AB/5; AB = 54/5
Всё. АВ = 54/5 = 10,8