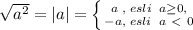
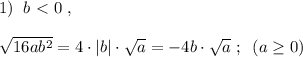
![2)\; \; b \leq 0\; ,\; \; \sqrt{150a^3b^6}= \sqrt{25\cdot 6\cdot a^2\cdot a\cdot (b^3)^2} =\\\\=3\cdot |a|\cdot |b^3|\cdot \sqrt{6a}=\\\\=[\; 6a \geq 0\; \to \; \; a \geq 0\; \to \; \; |a|=a\; ;\\\\\; b\leq 0\; \to \; \; b^3 \leq 0\; \to \; \; |b^3|=-b^3\; ]=\\\\=3a\cdot (-b^3)\cdot \sqrt{6a}=-3ab^3\sqrt{6a}](/tpl/images/0776/0443/285d7.png)

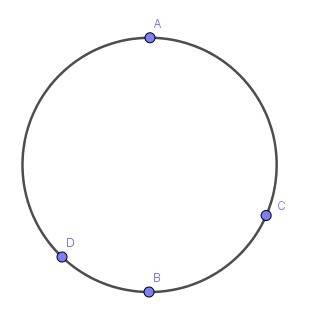
Обозначаю для простоты A, Б, В, Г через английские A,B,C,D
1) Расстояние от А до В будем отмечать в последнюю очередь.
Длина всей кольцевой дороги равна AC+CD+DA=25 + 25 + 30 = 80 км. А поскольку расстояние от А до В равен 40 км и длина всей кольцевой дороги 80 км, то В расположена на половине окружности.
BC =AB - AC =40 - 25 = 15 км
ответ: 15 км.
2) Расстояние от А до В будем отмечать в последнюю очередь.
Длина всей кольцевой дороги равна AC+CD+DA=15+25+30 = 70 км. А поскольку расстояние от А до В равен 35 км и длина всей кольцевой дороги 70 км, то В расположена на половине окружности.
BC =AB - AC =35 - 15 = 20 км
ответ: 20 км.