Объяснение:
2.
a) 3x+12>4x-1 | (-x>-13) /-1 | x<13
7-2x<=10-3x | -3 <= -x /-1 | x <= 13. x принадлежит (-∞; 13].
б) 2x-9 > 6x+1 | (-4x > 10) / -4 | x<10
( -
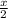< 2 ) *-2 | x > 4. x принадлежит (-∞; 10) и (4; +∞).
3.
а)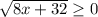 
Взводим все в квадрат
8x+32 => 0
8x => 32 делим все на 8
x => 4. x принадлежит [4; +∞).
б)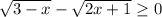 
Взводим все в квадрат
3-x-2x+1 => 0
4 => 3x Делим все на 3
1.3 => x
x <= 1.3. x принадлежит [-∞; 1.3).
4.
а-7 => 0 3-2a => 0
a => 7 3 => 2a
1.5 => a ответ: a принадлежит [7; +∞).
▪(а - b)(a^2 + ab + b^2) = a^3 - b^3 .
(1/2x-1/3y)(1/4x^2+1/6xy+1/9y^2) = (1/2x)^3 - (1/3y)^3 = 1/8x^3 - 1/27y^3
но если ошибки нет, тогда, что бы упростить, надо перемножить первую скобку на вторую:
(1/2x-1/3y)(1/4x^2+1/6xy+1/3y^2) = (1/2х)×(1/4x^2) + (1/2х)×(1/6xy) + (1/2х)×(1/3y^2) - (1/3y)×(1/4x^2) - (1/3y)×(1/6xy) - (1/3y)×(1/3y^2) = 1/8х^3 + 1/12(х^2)у + 1/6х(у^2) - 1/12(х^2)у - 1/18х(у^2) - 1/9у^3 = 1/8х^3 + (2ху^2)/18 - 1/9у^3 = (1/8)х^3 + (ху^2)/9 - (1/9)у^3