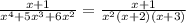
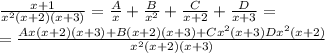
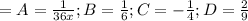
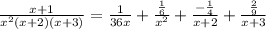
пусть пешеход, вышедший из А, после встречи км. Тогда его скорость v1=S/t =
= 3x/2 км/час (40 мин = 2/3 час).
Пешеходу, вышедшему из В, после встречи пришлось пройти x + 2 км. Тогда его скорость
v2=S/t = 2(x+2)/3 км/час (1 час 30 мин = 3/2 час).
До встречи первый затратил время t = (x+2)/v1 = 2 * (x+2)/(3x).
До встречи второй затратил время t = x/v2 = 3 * x/(2(x+2)). Времена затраченные до встречи равны. Составляем уравнение.
(2x + 4)/3x = 3x/(2x+4)
(2x + 4)² = 9x²
либо 2x + 4 = 3x. x=4, либо
2x + 4 = -3x. x=-4/5 (не имеет смысла).
Искомое расстояние S = x + x + 2 = 4 + 4 + 2 = 10 км
x2 + 4x + 8 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 42 - 4·1·8 = 16 - 32 = -16
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
4x2 - 12x + 9 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-12)2 - 4·4·9 = 144 - 144 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительных корень:
x = 122·4 = 1.5
3x2 - 4x - 1 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-4)2 - 4·3·(-1) = 16 + 12 = 28
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 4 - √282·3 = 23 - 13√7 ≈ -0.21525043702153024
x2 = 4 + √282·3 = 23 + 13√7 ≈ 1.5485837703548635
2x2 - 9x + 15 = 0 Найдем дискриминант квадратного уравнения: D = b2 - 4ac = (-9)2 - 4·2·15 = 81 - 120 = -39 Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
x^4+5x³+6x²=x²(x²+5x+6)=x²((x²+2x)+(3x+6))=x²(x(x+2)+3(x+2))=
=x²(x+2)(x+3)
(x+1)/(x^4+5x³+6x²)=A/x²+B/(x+2)+C/(x+3)+D/x
A*(x²+5x+6)+B*(x³+3x²)+C*(x³+2x²)+D*(x³+5x²+6x)=x+1
x³*(B+C+D)+x²*(A+3B+2C+5D)+x*(5A+6D)+6*A=x+1
{B+C+D=0
{A+3B+2C+5D=0
{5A+6D=1
{6A=1⇒A=1/6
подставим в 3
5/6+6D=1
6D=1-5/6=1/6
D=1/6:6=1/36
подставим в 1 и 2
{B+C=-1/36/*(-2)⇒-2B-2C=2/36
{3B+2C=-11/36
прибавим
B=-9/36=-1/4
C=-1/36+1/12=-1/36+3/36=2/36=1/18
Получили
1/(6х²)-1/(4(х+2))+2/(9(x+3))+1/(36х)=(х+1)/(х^4+5x³+6x²)