15 декабря
Объяснение:
Можно увидеть что это задача в которой присутствует арифметическая прогрессия, в которой:
d = 4
a₁ = 10
Sₙ (сумма какого то количества первых членов) = 640
Решаем при формулы суммы n первых членов арифметической прогрессии:
Sₙ =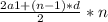 
(a1 это а₁)
Подставляем известные нам данные и решаем как уравнение:
640 =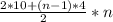 
640 = (10 + 2 * (n - 1)) * n
640 = 10n + 2n² - 2n
2n² + 8n - 640 = 0
Поделим обе части уравнения на 2 что бы упростить:
n² + 4n - 320 = 0
Найдем дискриминант:
D = 16 - 4 * 1 * (-320) = 1296
x₁ =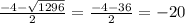 
(нам не подходит ибо количество дней не может быть отрицательным)
x₂ =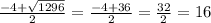 
(дней)
31 - 16 = 15 (декабря)
Здесь можно пойти двумя путями.
1) Через формулу квадрата разности (раскрыть первые скобки и решить уравнение). Выглядит она следующим образом: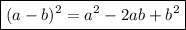 
2) Через формулу разности квадратов (т.к. мы замечаем, что и уменьшаемое, и вычитаемое имеют четную степень). Выглядит она следующим образом: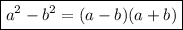 
.
Первый вариант решения.
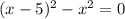
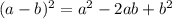раскрываем скобк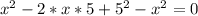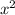и.
и 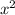взаимно сокращаются, т.к. имеют противоположные знаки, после чего решаем уравнение как обычно.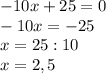
ответ: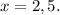 
Второй вариант решения.
.
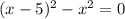
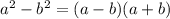ответ: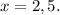
(2/7-1/14)*(3,5-17,5)=(4/14-1/14)*(-14)=3/14*(-14)=-3
2
15*32/(34^2-14^2)=15*32/[(34-14)(34+14)]=15*32/(20*48)=1/2=0,5
3
-4*(2,5x+2,4)+(5x+4)=0,4
-10x-9,6+5x+4=0,4
5x=-5,6-0,4
5x=-6
x=-6:5
x=-1,2
4
(3a-5b)*(3a+5b)=9a²-25b²