Третье решить не получается, прости
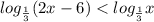
Так как основания логарифмов равны, мы можем их опустить и решать как обычное уравнение
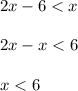
x ∈ ( -∞ ; 6 )
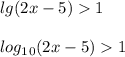
Из единицы нам нужно представить десятичный логарифм , чтобы как в первом уравнении их можно было опустить
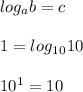
Теперь вместо единицы подставим логарифм
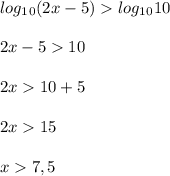
x ∈ ( 7,5 ; +∞ )
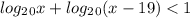
как и в предыдущем неравенстве, единицу представляем в виде логарифма с тем же основанием
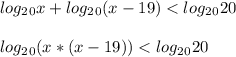
По свойству логарифма ⇒ logₐb + logₐc = logₐ ( b · c )
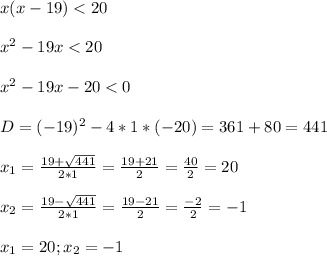
x < 20 ; x < -1
Подставим получившиеся значения в выражение, то есть сделаем проверку ( не всегда оба корня подходят )
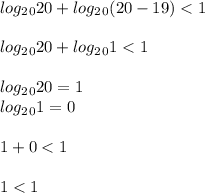
Так как по обе стороны значения получились одинаковыми, можно считать что решение верно ( беря числа меньше 20, неравенство будет верным )
Подставим второй корень
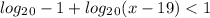
Сразу можно сказать что корень не подходит, так как логарифма отрицательного числа не бывает.
Остаётся только один корень
x < 20
x ∈ ( +∞ ; 20 )
Объяснение:
84%+36%=120%
у него было 100% своих денег,но когда бабушка добавила ему 150 рублей ему стало хватать,то есть у него стало 120% от своих денег,значит
1.) 120%-100%=20%
150 рублей это 20%,осталось посчитать сколько будет 86% и 36%
в уме модно посчитать ,что раз 150 рублей это 20%,то 1% это 150:2=75 рублей
теперь посчитаем сколько рублей равняется одному рублю
2.) 150:20=7,5 рубля=1 %
теперь считаем до 36%
36 % это :1 по 150 рублей ,1 по 75 рублей и 6 по 7,5 рублей
3.)150+75+7,5+7,5+7,5+7,5+7,5+7,5=270 рублей столько стоит коврик
также считаем с компьютерной мышью
4.)150×4+7,5×4=630 рублей,столько стоит мышь
ответ:630,270 рублей
ч.т.д
1) Промежутки монотонности, наибольшее и наименьшее значение
функции y=2x^2-x-6 на промежутке [-1;3];
График этой функции - парабола ветвями вверх.
Надо найти её вершину Хо = -в/2а = 1/4.
Уо = 2*(1/16)-(1/4)-6 = -98/16 = -6(1/8). Это минимальное значение.
Максимум - ∞.
Промежутки выпуклости функции y=2x^2-x-6 на промежутке [-1;3].
У параболы выпуклость только одна - в сторону вершины.
Для данной - выпуклость вниз.
2) Промежутки монотонности, наибольшее и наименьшее значение;
функции y=3x^2-x^3 на промежутке [-1;1].
Находим производную функции: y' = -3x² + 6x и приравняем её нулю:
-3х(х-2) = 0.
Имеем 2 критические точки: х = 0 и х = 2.
Это точки определяют 3 промежутка знака производной функции.
Где производная положительна - там функция возрастающая, где отрицательна - там функция убывающая.
x = -1 0 1 2 3
y' = -3x² + 6x -9 0 3 0 -9.
Функция возрастающая: х ∈ (-∞; 0) ∪ (2; +∞).
Функция убывающая: х ∈ (0; 2).
Промежутки выпуклости функции y=3x^2-x^3 на промежутке [-1;1].
Находим вторую производную y'' = -6x + 6.
-6(x - 1) = 0.
Точка перегиба х = 1.
х = 0 2
y'' = 6 -6.
Функция выпукла вниз: х ∈ (-∞; 1).
Функция выпукла вверх: х ∈ (1; +∞).