1. Укажите линейное уравнение с двумя переменными.
1) 3·x-5=0 - только одна переменная х
2) х/7-у/5=8/3 - линейное, переменные х и у
3) 7/х+5/у=3/8 - нелинейное
4) 7·x²+5·у=3 - уравнение 2-степени
2. Укажите уравнение, решением которого является пара чисел (1 3/7; 2 5/6) .
Проверим подставкой в уравнение:
1) 14·x-12·y+14=0
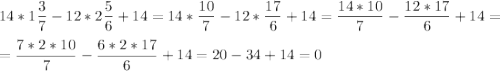
является решением, поэтому остальные уравнение не нужно проверить
2) 14·x-6·y-10=0
3) 10·x/7+17·y/6=27
4) x-6·y=17
3. Какая пара чисел является решением уравнения 3·x-2·y+5=0
1) (-1/3; -2) 2) (-2; -1/3) 3) (-4/3; -1/2) 4) (-3; 2)
Проверим подставкой в уравнение:

не является решением
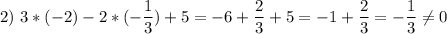
не является решением
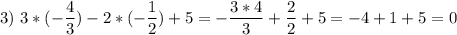
является решением, поэтому последнюю пару не нужно проверить
4. Какая из пар чисел является решением уравнением 2·x-y=6
1) (2; -1) 2) (5; 3) 3) (1; -4) 4) (-1; -3)
Проверим подставкой в уравнение:
1) 2·2-(-1)=4+1=5≠6 - не является решением
2) 2·5-3=10-3=7≠6 - не является решением
3) 2·1-(-4)=2+4=6=6 - является решением, поэтому последнюю пару не нужно проверить
2sin (40°+x)sin(x-50°)+1=0
sin (40°+x)sin(x-50°)=-1/2
1/2*[cos(40+x-x+50)-cos(40+x+x-50)]=-1/2
cos90-cos(2x-10)=-1/2
cos(2x-10)=1/2
2x-10=-60+360k U 2x-10=60+360k
2x=-50+360k U 2x=70+360k
x=25+180k U x=35+180k,k∈z
2
4cos^2x+sinxcosx+3sin^2x-3=0
4cos²x+sinxcosx+3sin²x-3cos²x-3sin²x=0
cos²x+sinxcosx=0
cosx(cosx+sinx)=0
cosx=0⇒x=π/2+πk,k∈z
cosx+sinx=0/cosx
1+tgx=0
tgx=-1⇒x=-π/4+πk,k∈z
3
cos^2x-3sinxcosx=-1
cos²x-3sinxcosx+sin²x+cos²x=0 /cos²x
tg²x+3tgx+2=0
tgx=a
a²+3a+2=0
D=9-8=1>0
a1+a2=-3 U a1+a2=2
a1=-2⇒tgx=-2⇒x=-arctg2+πk,k∈z
a2=-1⇒tgx=-1⇒x=-π/4+πk,k∈z