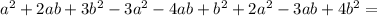

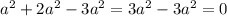
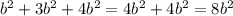
 - Тут вынес знак минуса за скобку, чтобы было понятно, что разность -4ab-3ab дает сумму с отрицательным знаком.
- Тут вынес знак минуса за скобку, чтобы было понятно, что разность -4ab-3ab дает сумму с отрицательным знаком.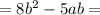
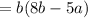
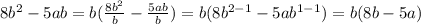

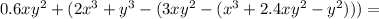
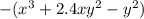 "
"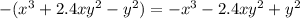

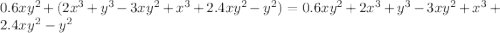

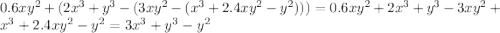
ответ:
1) cos x = 1/2 1) sin x = -1/2
2) sin x = -/2 2) cos x = /2
3) tg x = 1 3) ctg x = -1
4) cos (x+) = 0 4) sin (x – /3) = 0
5) 2 cos x = 1 5) 4 sin x = 2
6) 3 tg x = 0 6) 5 tg x = 0
7) sin 4x = 1 7) cos 4x = 0 пример. 4 – cos2 x = 4 sin x
так как cos2 x = 1 – sin2 x, то
4 – (1 – sin2 x) = 4 sin x,
3 + sin2 x = 4 sin x,
sin2 x - 4 sin x + 3 = 0,
пусть y = sin x, получим уравнение
y 2 - 4 y +3 = 0
у1=1; у2=3.
sin x =1 или sin x = 3,
x = /2 + 2 n, n= z, решений нет.
ответ: x = /2 + 2 n, n= z.
объяснение:
Представим, что выбранные монеты пожертвовали рубль на благотворительность, а потом решили отдать туда же половину своего номинала.
После первого процесса сумма уменьшилась на 11 и стала равна 14 рублям, а номиналы монет стали 0, 2 и 4 рубля, после второго - сумма стала в два раза меньше (7 рублей), а новые номиналы - 0, 1 и 2 рубля.
Итак, нужно найти все выдать 7 рублей 11 монетами по 0, 1 и 2 рубля. Понятно, что двухрублёвых монет должно быть не больше трёх - иначе сумма была бы больше 4 * 2 = 8 рублей, а на самом деле всего 7.
Перебираем варианты:
- нет двухрублевых монет. Надо выдать 7 рублей - это 7 монет по 1 рублю и 11 - 0 - 7 = 4 монеты по 0 рублей.
- одна двухрублевая монета. Осталось выдать 5 рублей - 5 монет по 1 рублю и 11 - 1 - 5 = 5 монет по 0 рублей.
- две монеты по 2 рубля. Осталось выдать 3 рубля - 3 монеты по 1 рублю, 11 - 2 - 3 = 6 монет по 0 рублей.
- три монеты по 2 рубля. Осталось выдать 1 рубль - 1 монета по 1 рублю, 11 - 3 - 1 = 7 монет по 0 рублей.
А теперь монеты одумались и забрали свои пожертвования обратно. Получились четыре заплатить 25 рублей:
- 0 по 5₽ + 7 по 3₽ + 4 по 1₽
- 1 по 5₽ + 5 по 3₽ + 5 по 1₽
- 2 по 5₽ + 3 по 3₽ + 6 по 1₽
- 3 по 5₽ + 1 по 3₽ + 7 по 1₽