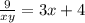
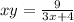
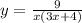
2 (км/час) - скорость течения реки
Объяснение:
х - скорость течения реки
9+х - скорость лодки по течению
9-х - скорость лодки против течения
77/(9+х) - время лодки по течению
77/(9-х) - время лодки против течения
По условию задачи на путь по течению затрачено на 4 часа меньше, уравнение:
77/(9-х) - 77/(9+х) = 4
Избавляемся от дробного выражения, общий знаменатель (9-х)(9+х) или 81-х², надписываем дополнительные множители над числителями:
77(9+х) - 77(9-х)=4(81-х²)
693+77х-693+77х=324-4х²
4х²+154х-324=0/4 разделим уравнение на 4 для удобства вычислений:
х²+38,5х-81=0
х₁,₂=(-38,5±√1482,25+324)/2
х₁,₂=(-38,5±√1806,25)/2
х₁,₂=(-38,5±42,5)/2
х₁= -81/2= -40,5 отбрасываем, как отрицательный
х₂= 4/2=2 (км/час) - скорость течения реки
Проверка:
77: 11=7 (часов) время по течению
77 : 7=11 (часов) время против течения
11-7=4 (часа) - разница, всё верно.
Объяснение:
2)-x²+x+72>0
x²-x-72=0
х₁,₂=(1±√1+288)/2
х₁,₂=(1±√289)/2
х₁,₂=(1±17)/2
х₁= -16/2= -8
х₂=18/2=9
x∈(-8; 9)
Решения неравенства находятся в области от -8 до 9.
4)x²+x-210<=0
x²+x-210=0
х₁,₂=(-1±√1+840)/2
х₁,₂=(-1±√841)/2
х₁,₂=(-1±29)/2
х₁= -30/2= -15
х₂=28/2=14
x∈(-15; 14)
Решения неравенства находятся в области от -15 до 14.
6)25x²+90x+81<=0
25x²+90x+81=0
х₁,₂=(-90±√8100-8100)/50
х₁,₂=(-90±√0)/50
х₁,₂= -90/50= -9/5
x> -9/5
8)36x²-84x+49>0
36x²-84x+49=0
х₁,₂=(84±√7056-7056)/72
х₁,₂=(84±√0)/72
х₁,₂=84/72=7/6
x<7/6