Графики функций у=kx+l и y=x²+bx+c при k= -3; l= -8; b=7; c=16 пересекаются в точках A(-4; 4) и B(-6; 10).
Объяснение:
у=kx+l y=x²+bx+c A(-4; 4); B(-6; 10)
1)Составим уравнение прямой у=kx+l по формуле:
(х-х₁)/(х₂-х₁) = (у-у₁)/(у₂-у₁)
Значения х и у - координаты точек.
х₁= -4 у₁=4
х₂= -6 у₂=10
Подставляем значения х и у в формулу:
(х-(-4)/(-6)-(-4) = (у-4)/(10-4)
(х+4)/(-2) = (у-4)/6 перемножаем крест-накрест, как в пропорции:
6х+24= -2у+8
2у= -6х+8-24
2у= -6х-16
у= -3х-8, искомое уравнение.
k= -3 l= -8.
2)y=x²+bx+c A(-4; 4); B(-6; 10)
Используя координаты данных точек, составим систему уравнений:
4=(-4)²+b*(-4)+c
10=(-6)²+b*(-6)+c
Произвести необходимые действия:
4=16-4b+c
10=36-6b+c
Выразим с через b в двух уравнениях:
-с=16-4b-4 -с=12-4b
-c=36-6b-10 -c=26-6b
Приравняем правые части уравнений, так как левые равны:
12-4b=26-6b
-4b+6b=26-12
2b=14
b=7
Теперь вычислим с:
-с=12-4b
-с=12-4*7
-с=12-28
-с= -16
с=16
Подставляем полученные значения b и c в уравнение:
у=x²+7x+16, искомое уравнение.
Число делится на 10 только в том случае, если оно оканчивается цифрой 0.
Посмотрим, какой цифрой оканчивается каждое слагаемое.
1) число 7 в разных степенях оканчивается разными цифрами. Попробуем установить закономерность.
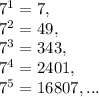
Т.е. последние цифры записи степеней семерки чередуются так: 7 - 9 - 3 - 1 и по кругу.
Т.к.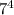 
оканчивается цифрой 1, то 
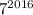также оканчивается цифрой 1. Тогда число 
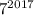оканчивается цифрой 7.
2) Для степеней четверки закономерность проще - 4 - 6 и по кругу:
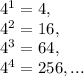
Поскольку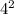 
оканчивается цифрой 6, то 
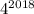также оканчивается цифрой 6.
3) Закономерность для степеней тройки - 3 - 9 - 7 - 1 и по кругу:
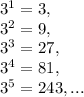
Т.к.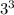 
оканчивается цифрой 7, то 
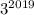также оканчивается цифрой 7.
В итоге слагаемые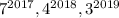 
оканчиваются цифрами 7, 6 и 7 соответственно. Если их сложить, то в разрядке единиц класса единиц получим 0. Т.е. число 
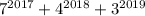оканчивается цифрой 0 - следовательно, оно таки делится на 10.
ОТВЕТ: да.
2)(32*a^2*c^3+27*c-48*a^6-288*a^3)/(48*a^2)