490 мин
Объяснение:
Весь круг циферблата часов разделён на 60 минутных делений.
За 1 час минутная стрелка проходит эти 60 делений. В то же время часовая стрелка проходит 5 делений.
Тогда скорость конца минутной стрелки 1 дел /мин, а часовой стрелки 1/12 дел/ мин.
От 3.50 до 4-х часов пройдёт 10 минут
Начнёи теперь двигаться от 16,00 .
1-й раз стрелки встретятся между 16.00 и 17.00
2-й раз между 17.00 и 18.00
И так далее.
8-й раз стрелки встретятся между 11.00 и 12.00
При этом от 11.00 до 12.00 минутная стрелка пройдёт 55 делений и ещё х делений, а минутная стрелка за то же время х делений
Составим уравнение (55 + х) : 1 = х : 1/12
55 + х = 12х
11х = 55
х = 5
Получилось, что при движении минутная стрелка делений, а минутная 5 делений. Это означает, что в 8-й раз минутная и часовая стрелка встретятся ровна в 12 часов.
12час - 3час 50мин = 8час 10мин = 490 мин
Часовая стрелка проходит 5 делений циферблата в час, минутная - 60 делений.
За минуту часовая проходит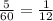 
часть деления, минутная - 1 деление. Значит за 1 минуту минутная стрелка "догоняет" часовую на 
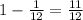часть деления.
В настоящий момент стрелки разделяет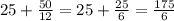 
деления (см. рис. - считаем по часовой стрелке).
Когда минутная стрелка в первый раз поравняется с часовой, ей нужно будет "догнать" часовую ещё 7 раз, сократив расстояние на 60 делений, то есть всего на 60·7 = 420 делений.
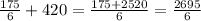делений нужно пройти минутной стрелке, чтобы в восьмой раз поравняться с часовой.
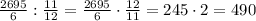минут понадобится, чтобы минутная стрелка в восьмой раз поравнялась с часовой
Одна из формул: Площадь треугольника равна половине произведения соседних сторон на синус угла между ними.
В прямоугольном треугольнике АВР гипотенуза АВ=ВР:cos60°=2BP
В прямоугольном треугольнике ВМС гипотенуза ВС=ВМ:cos60°=2ВМ
S ∆ BMP=BM•BP•sin60°:2=10
S ∆ BMP=BM•BP•√3/4=10⇒
BM•BP•√3=40
S ∆ ABC=2BP•2BM•sin60°:2⇒
S ∆ ABC =4 BP•BM√3:4=BM•BP•√3
BM•BP•√3=40 (см. выше)⇒
Площадь ∆ АВС=40 ед. площади.
-------
Заметим, что по первой лемме о высотах (Если в треугольнике ABC нет прямого угла, АА1 и ВВ1 ( здесь AР и СМ ) – его высоты, то ∆ А1В1С подобен ∆ ABC. (здесь ∆ МВР~∆ABC) ∆ АВС и МВР подобны с коэффициентом подобия k=ВР:АВ=2
Отношение площадей подобных треугольников равно квадрату коэффициента их подобия, следовательно,
S ∆ ABC:S∆ MBP=k²=4⇒
S ∆ ABC=4 S∆ MBP=40 ед. площади