1.Хп=(3n+1)/n=3+1/n
пользуясь свойствами обратной пропорциональности
(монотонно спадающая)
ограниченна сверху первым членом 4=3+1/1
ограничена снизу 3=3+0 (при n->бесконечность 1/n->0)
2.Xn=4n
пользуясь свойствами линейной функции
(монотонно возрастающая)
сверху неограниченна
((при n->бесконечность 4n->бесконечность)
ограниченна снизу первым членом 4=4*1
3.Xn=(0.25)^n
пользуясь свойствами експоненциальной функции
(монотонно убывающая)
ограниченна сверху первым членом 0.25=0.25^1
ограниченна снизу 0 (при n->бесконечность (0.25)^n->0)
4.Xn=(-0.5)^n
пользуясь свойствами експоненциальной функции
ограниченна снизу первым членом -0.5=(-0.5)^1
ограниченна сверху вторым членом 0.25=(-0.5)^2
а) sin x - 0,5 = 0
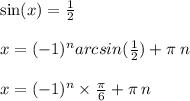
*где n - целое число
Рассмотрим варианты:
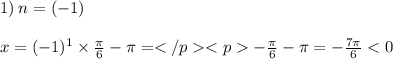
При n=(-1) - х<0 и не принадлежит отрезку [0;2π].
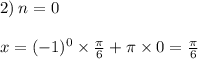
При n=0 - x = π/6 - принадлежит отрезку [0;2π].
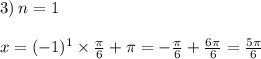
При n=1 - x = (5π/6) - принадлежит отрезку [0;2π].
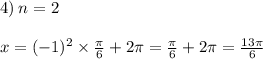
При n=2 - x = (13π/6) - не принадлежит отрезку [0;2π].
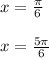
б) tg x - 1 = 0
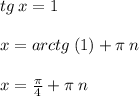
*где n - целое число
Рассмотрим варианты:
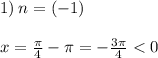
При n=(-1) - х<0 и не принадлежит отрезку [0;2π].
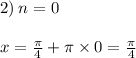
При n=0 - x = π/4 - принадлежит отрезку [0;2π].
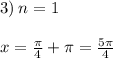
При n=1 - x = (5π/4) - принадлежит отрезку [0;2π].
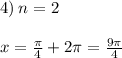
При n=2 - x = (9π/4) - не принадлежит отрезку [0;2π].
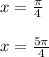
![Найдите корни уравнения, принадлежащие отрезку [0;2пи]: а) sin x - 0,5 = 0; б) tg x - 1 = 0.](/tpl/images/4836/4198/1fe1b.jpg)
площадь отрезанного прямоугольника = а*в
площадь остатка = - а*в = а(а-в)