В иррациональных уравнениях кроме ОДЗ нужно всегда учитывать дополнительные условия (ДУ) или всегда для проверки подставлять полученные корни в исходное уравнение.
Рассмотрим исходное уравнение: 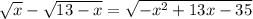
Далее мы возводим это уравнение в квадрат, но это неэквивалентный переход - например, неправильное равенство -1 = 1 переходит в правильное 1 = 1, поэтому на этом этапе легко приобрести лишние корни, что и произошло.
В правой части исходного уравнения находится неотрицательный корень, поэтому в ДУ необходимо потребовать неотрицательность левой части: 
Как раз это ДУ и позволяет в процессе решения откинуть лишний корень 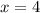
Пусть х км в час - скорость первого, у км в час - скорость второго.
1 мин = (1/60) часа
За 1 мин первый проехал (х/60) км,
второй (y/60) км
Первый проехал на 146 м =0,146 км больше, поэтому
(x/60)- (y/60)=0,146 ⇒ x-y=0,146*60 ⇒ y=x-8,76
Путь пройденный первым за 1 минуту равен (1/120) всей трассы
x/60 =S/120 ⇒ S=2x
Первый проехал дистанцию 2х км со скоростью х км в час
за (S/x)=(2x/x)=2 часа.
и финишировал на 30 мин раньше, чем второй.
Значит второй проехал (2x-0,146) км за 2,5 часа со скоростью
y=x-8,76
Уравнение:
(2x-0,146) =2,5*(х-8,76)
2х-0,146=2,5х-21,9
0,5х=21,9-0,146
х=43,508 км в час
x = 4/5 + 2/5y
5(Х+3)-8(У-2)=13
подставить значение x в другое уравнение:
x = 4/5 + 2/5y
5(4/5 + 2/5y +3)-8(y-2)=13
когда мы это решили мы узнаём, что y = 7/3
x = 4/5 + 2/5 * 7/3
x = 2/15
ответ:(2/15;7/3)