Выполните действия: а)x^11x^12x; б)y^15: y^3; в)(xyz)^4; г)(a^-3)5; д)3^-53^4; выражение; a)(3ab-5a--3a); b)2x^2(3-5x^2); g)(2a+b)(2a-b); d)(3x+y)^2; e)(x^2+y^2)^2; выражение: a)(a-4)(a-2)+(a+1)(a+3) сократите дробь: a)14a^4b/49a^3 b^2; b)y^2-z^2/2y+2z; выполните действия; a) (a/a+4-a/a-4)*a+4/a выражение: (y^2-2y)^2-y^2(y+3)(y-3)+2y(2y^2+5) мозги не варят))

👇

Ответ:

FOXI66666

13.10.2021

X^11*x^12*x=x^24
y^15:y^3=y^12
(xyz)^4=x⁴y⁴z⁴

(3ab-5a-b)-(12ab-3a)=3ab-5a-b-12ab+3a=
-9ab-2a-b
2x^2(3-5x^2)=6x²-10x⁴
(2a+b)(2a-b)=4a²-b²
(3x+y)^2=9x²+6xy+y²
(x^2+y^2)^2=x⁴+2x²y²+y⁴

(a-4)(a-2)+(a+1)(a+3)=a²-2a-4a+8+a²+3a+a+3=2a²-2a+11

14a^4b/49a^3b^2=2a/7b
y^2-z^2/2y+2z=(y-z)(y+z)/2(y+z)=(y-z)/2

(a/a+4-a/a-4)*a+4/a=a/a*a+4a-a/a*a-4a+4/a=a-a+4/a=4/a

(y^2-2y)^2-y^2(y+3)(y-3)+2y(2y^2+5)=
y⁴-4y³+4y²-y²(y²-9)+4y³+10y=y⁴+4y²-y⁴+9y²+10y=3y⁴+12y²+10y

4,6(58 оценок)

Открыть все ответы

Ответ:

FROST22223333

13.10.2021

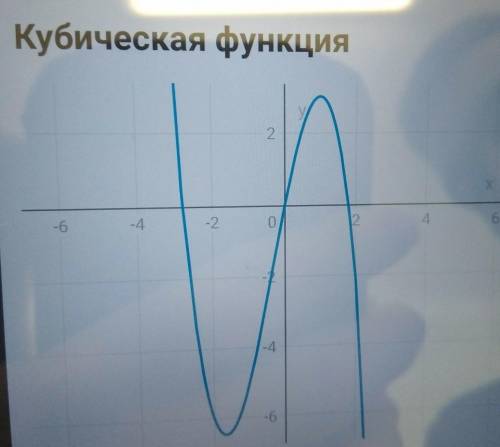
ответ: для начала нам надо найти точки экстремума. для этого найдем производную и приравняем её к 0. получаем -3х^3-2х+5 =0. получаем корни и запоминаем их. далее нам надо найти интеграл от этой производной. поскольку нам крупно повезло мы получаем функцию аналогичную начальной. подставляя числа в промежутке от -5 до 2 получаем такой график функции, при этом, не забываем про производную которую мы находили и проверяем попали ли высоты в значения производной по оси Х, потом подставляем производную в начальное уравнение и получаем значения по У. подставляем эти значения в оси и получаем места перегиба графика. у нас всё получилось

4,5(70 оценок)

Ответ:

Danil0220

13.10.2021

Начнем с того, что я выпишу все формулы, которые я буду использовать здесь.
1. Разность квадратов.
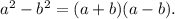
a^2-b^2=(a+b)(a-b).

2. Приведение дробей к общему знаменателю.
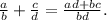
$\frac{a}{b}+ \frac{c}{d}= \frac{ad+bc}{bd}.$
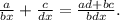
Причем, если знаменатели имеют общий множитель, то на него можно и не домножать. Как к примеру тут: $\frac{a}{bx}+ \frac{c}{dx}= \frac{ad+bc}{bdx}.$
3. Квадрат разности.
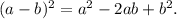
(a-b)^2=a^2-2ab+b^2.

4. Умножение дробей.
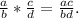
$\frac{a}{b}* \frac{c}{d}= \frac{ac}{bd}.$
(Числитель умножаем с числителем, а знаменатель - со знаменателем.)
5. Деление дробей.
$\frac{a}{b}: \frac{c}{d}= \frac{a}{b}* \frac{d}{c}= \frac{ad}{bc}.$
(Вторую дробь (делитель) переворачиваем, а знак деления заменяем умножением.)
6. Умножение многочлена на многочлен.
Чтобы умножить два многочлена между собой, надо каждый член первого многочлена умножить на каждый член второго многочлена.
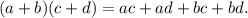
(a+b)(c+d)=ac+ad+bc+bd.

1). Преобразуем немного наше выражение.
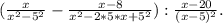
$( \frac{x}{x^2-5^2}- \frac{x-8}{x^2-2*5*x+5^2}): \frac{x-20}{(x-5)^2} .$
2). Видно, что в знаменателе первой дроби можно использовать формулу разности квадратов, а в знаменателе второй дроби полный квадрат (квадрат разности). Применим эти формулы.
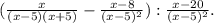
$(\frac{x}{(x-5)(x+5)}- \frac{x-8}{(x-5)^2}): \frac{x-20}{(x-5)^2}.$
3). Приведем первые две дроби общему знаменателю.
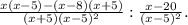
$\frac{x(x-5)-(x-8)(x+5)}{(x+5)(x-5)^2} : \frac{x-20}{(x-5)^2}.
$
4). Раскрываем скобки в числителе первой дроби.
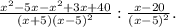
$\frac{x^2-5x-x^2+3x+40}{(x+5)(x-5)^2} : \frac{x-20}{(x-5)^2}.$
5). Приводим подобные слагаемые.
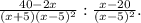
$\frac{40-2x}{(x+5)(x-5)^2} : \frac{x-20}{(x-5)^2}.$
6). Делим, а затем умножаем дроби.
$\frac{40-2x}{(x+5)(x-5)^2} * \frac{(x-5)^2}{x-20}= \frac{(40-2x)(x-5)^2}{(x+5)(x-5)^2(x-20)} .$
7). Сокращаем дроби и выносим общий множитель (-2) в числителе.
$\frac{(40-2x)}{(x+5)(x-20)}= \frac{-2(x-20)}{(x+5)(x-20)} .$
8). Опять сокращаем.
$\frac{-2}{x+5}=- \frac{2}{x+5} .$
ответ: $- \frac{2}{x+5}.$