Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру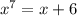 
уравнение в действительных корнях.
Рассмотрим функцию 
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию 
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение 
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
Объяснение:
Функция задана формулой y = −3x + 1. Определите:
1) значение функции, если значение аргумента равно 4;
2) значение аргумента, при котором значение функции равно −5;
3) проходит ли график функции через точку A (−2; 7).
1)y = −3x + 1
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у 4 1 -2
а)Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=4
у= -3*4+1= -11 при х=4 у= -11
б)Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у= -5
-5= -3х+1
3х=1+5
3х=6
х=2 у= -5 при х=2
в)Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
A (−2; 7)
y = −3x + 1
7= -3*(-2)+1
7=6+1
7=7, проходит.
2)Постройте график функции y = 2x − 5. Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно 3;
2) значение аргумента, при котором значение функции равно −1.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y = 2x − 5
Таблица:
х -1 0 1
у -7 -5 -3
б)согласно графика, при х=3 у=1
согласно графика у= -1 при х=2
3)Не выполняя построения, найдите координаты точек пересечения
графика функции y = −0,6x + 3 с осями координат.
а)График пересекает ось Оу при х=0:
х=0
у= -6*0+3=3
Координаты точки пересечения графиком оси Оу (0; 3)
б)График пересекает ось Ох при у=0.
у=0
0= -0,6х+3
0,6х=3
х=5
Координаты точки пересечения графиком оси Ох (5; 0)
4)При каком значении k график функции y = kx+ 5 проходит через точку D (6; −19)?
Подставляем известные значения х и у (координаты точки D) в уравнение и вычисляем k:
y = kx+ 5
-19=k*6+5
-6k=5+19
-6k=24
k= -4
7x+2x=30-3
9x=27
x=3
2.) 3(x-2)=x+2
3x-6=x+2
3x-x=2+6
2x=8
x=4
3.) 5-2*(x-1)=4-x
5-2x+2=4-x
-2x+x=4-5-2
-x=-3
x=3
4.) 0.2x+2.7=1.4-1.1x
0.2x-1.1x=-1.4-2.7
-0.9x=-1.3
x=1.4
5.) 0.2(7-2y)=2.3-0.3(y-6)
1.4-0.4y=2.3-0.3y+1.8
-0.4y+0.3y=2.3+1.8-1.4
-0.1y=2.7
y=-27