Пусть число записано в виде произведения степеней простых множителей:
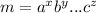, где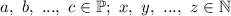 
Тогда, число делителей этого числа определяется по формуле:
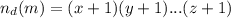
Рассмотрим некоторое число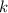 
. Пусть 
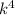имеет 85 делителей. Разложим число 85 на множители:
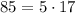
Заметим, что число 85 раскладывается на какие бы то ни было множители единственным образом.
Зная это, необходимо рассмотреть две ситуации.
1) Число делителей находилось как произведение из одного множителя (условное произведение):
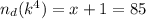
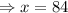
Тогда, число 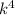имеет вид:
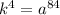
Найдем число :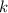
![k=\sqrt[4]{a^{84}}](/tpl/images/1399/3019/a4e5c.png)
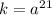
Найдем число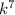 
:
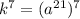
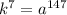
Число делителей этого числа:
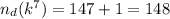
2) Число делителей находилось как произведение из двух множителей:
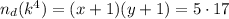
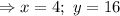
Тогда, число 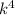имеет вид:
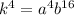
Найдем число :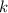
![k=\sqrt[4]{a^4b^{16}}](/tpl/images/1399/3019/39b3e.png)
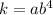
Найдем число :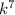
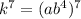
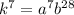
Число делителей этого числа:
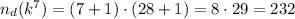
ответ: 148 или 232
b₂+b₄=20 b₁q+b₁q³=20 b₁q*(1+q²)=20
Разделим второе уравнение на первое:
q=2.
ответ:q=2.