В решении.
Объяснение:
Объяснение:
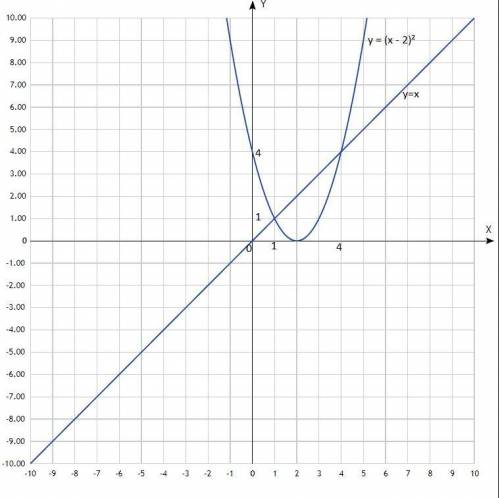
Решить графически систему уравнений:
y = (x - 2)²
y = x
Первый график - парабола со смещённым центром, второй - прямая, проходящая через начало координат.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
y = (x - 2)² y = x
Таблицы:
х -1 0 1 2 3 4 5 х -1 0 1
у 9 4 1 0 1 4 9 у -1 0 1
По вычисленным точкам построить графики.
Согласно построению, координаты точек пересечения: (1; 1); (4; 4).
Решения системы уравнения: (1; 1); (4; 4).
непонятно...
3-3(1)
81-3(4)
27-3(3)
243-3(5)
729-3(6)
чтобы возвести в 3 степень например 27,тебе нужно 3*3*3=27
значит 27 в степени 3,будет 3(3)