В решении.
Объяснение:
у=7х2+21х
побудувати графік, знайти вершину, вітки,область значення та визначення, функція зростає та спадає,проміжки знак осталості,найменше та найбільше значення
у = 7х² + 21х;
Построить график, найти вершину, направление ветвей, область определения и область значений, промежутки возрастания и убывания функции, промежутки знакопостоянства, наибольшее и наименьшее значение функции.
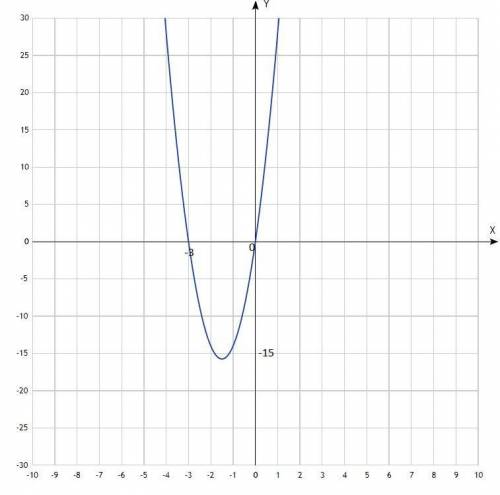
а) График - парабола, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -4 -3 -2 -1 0 1
у 28 0 -14 -14 0 28
По вычисленным точкам построить параболу.
Парабола пересекает ось Ох в точках х = -3; х = 0 (нули функции).
б) Найти координаты вершины параболы;
Формула: х₀ = -b/2a
x₀ = -21/14
x₀ = -1,5;
у₀ = 7 * (-1,5)² + 21 * (-1,5) = 15,75 - 31,5 = -15,75;
Координаты вершины параболы: (-1,5; -15,75).
в) Найти область определения;
Область определения - это проекция графика функции на ось Ох.
Обозначается как D(f) или D(у).
Область определения параболы - множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.
Обычно запись: D(f) = R.
г) Найти область значений функции;
Область значений - это проекция графика на ось Оу.
Обозначается как Е(f) или Е(y).
Область значений параболы определяется координатами вершины, конкретно у₀, значение у вершины параболы.
у₀ = -15,75;
Е(f) = у∈ R : у >= -15,75
у может быть любым, только >= -15,75.
д) Найти промежутки возрастания и убывания функции;
Функция возрастает при х∈(-1,5; +∞);
Функция убывает при х∈(-∞; -1,5).
е) Найти промежутки знакопостоянства;
у > 0 (график выше оси Ох) при х∈(-∞; -3)∪(0; +∞);
у < 0 (график ниже оси Ох) при х∈(-3; 0).
ж) у наиб. не существует;
у наим. = -15,75.
1. Обратно пропорциональная зависимость :
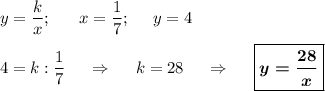
2. Решите графически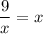 
График функции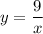 
- гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
x -9 -4,5 -3 -2 -1 1 2 3 4,5 9
y -1 -2 -3 -4,5 -9 9 4,5 3 2 1
График функции y = x - прямая линия, проходящая через начало координат. Точки для построения
x 0 2
y 0 2
ответ : (-3; -3) и (3; 3) - рис. 1.
3. Графически, сколько решений имеет уравнение 
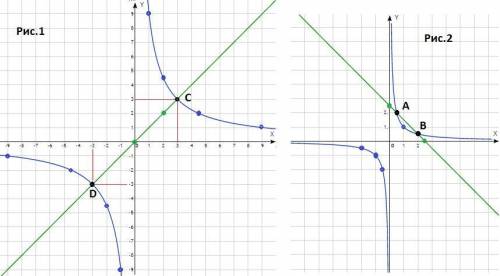
График функции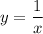 
- гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
x -2 -1 -0,5 0,5 1 2
y -0,5 -1 -2 2 1 0,5
График функции y = 2,5 - x - прямая линия. Точки для построения
x 0 2,5
y 2,5 0
ответ : уравнение имеет 2 решения - рис. 2.
ответ:
хуавей : 41%, apple : 0.8%,ксяоми : 43%,
самсунг: -11%