Очевидно, задача сводится к нахождению ежедневного заработка двумя мастерами. Если один получает х тг, а второй у тг в день, то вместе за день они получают х+у, если бы это были не переменные, а простые числа, вы бы тоже складывали, сложили, приравняли к тому численному значению, который получили. И есть еще одно соотношение, тот, который получает ежедневно х тг, за пять дней НА СКОЛЬКО БОЛЬШЕ ОН ПОЛУЧАЕТ, чем тот, который получает ежедневно у тг, за 4 дня своей работы. Это разностное сравнение. Вы от большего отнимаете меньшее, т.е. от 5х отнимаете 4у, и приравниваете к тому, что дано по условию. Составлена система. Дальше ее надо решить. Т.е. найти х и у. Вы ее решали методом подстановки, мне больше нравится метод сложения. Давайте его разберем с Вами.
х+у=16000
5х-4у=17000
Умножим первое уравнение на 4 и сложим со вторым. чтобы перейти к уравнению с одной буквой, например х. Получим
4х+4у=16000*4
5х-4у=17000
9х=17000+640000
9х=81000
х=9000
Значит, первый за день получает 9000 тг, тогда второй у=15000-х=16000-9000=7000 /тг/
ответ9000 тг, 7000 тг.
Теперь. в чем состоит метод подстановки? От системы надо опять таки перейти к уравнению с одной буквой. Вы из первого уравнения нашли х, можно было находить у, это все равно. Что удобнее. Но здесь абсолютно одинаково. например, х выразили из первого уравнения. получили х=16000-у, подставили его во второе уравнение. т.е. 5х-4у=17000, получили 5*(16000-у)=17000, ушли от системы и решаете теперь уравнение с одной буквой у. Получаете 5*16000-5*у-4у=17000; 80000-17000=9у; у=63000/9=7000, значит, 7000 тг получает второй, тогда первый подставим в любое из двух уравнений системы вместо у 7000, проще в первое уравнение, числа меньше, получим. 16000-7000=9000/тг/ - заработок первого. ФИНИШ.
Задавайте вопросы. Что не ясно?
Разобьем числа от 1000 до 9999 на следующие группы:
от 1000 до 1999, от 2000 до 2999, ..., от 9000 до 9999.
В каждой группе, очевидно, на первом месте стоит ненулевая цифра, поэтому их можно без каких-либо проблем отбросить. Отбросив их все, мы получим 9 совершенно одинаковых групп вида:
000, 001, 002, ..., 999.
Найдем количество нулей в одной такой группе.
Заметим, что эта группа представляет собой набор всевозможных упорядоченных последовательностей из трех цифр. Таким образом, можно сделать вывод, что каждая цифра в этом наборе написана одинаковое количество раз.
Всего в группе 000, 001, 002, ..., 999 имеется 1000 последовательностей, соответственно для их записи использовано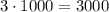 
цифр. Значит, каждая из десяти цифр записана по 
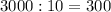раз.
Итак, цифра 0, как и любая другая цифра встречается в одной группе 300 раз. Значит, в девяти таких группах она встречается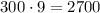 
раз.
ответ: 2700
Тогда х+(х+37)=180
2х=180-37
х=143:2
х=71.5 180-х=129.5
а) 71.5 и 129.5
2+7=9 частей
180:9=20 град - 1 часть
20*2=40
20*7=140
б) 40 и 140 град