Объяснение:
1. Чтобы выражение имело смысл, знаменатель не должен быть равен 0 (либо положительный, либо отрицательный). Значит, x - 3 
0.
x 3.
ответ: выражение имеет смысл при х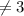 
.
2.1)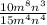 
. Сокращаем 10 и 15 на 5, а также вспоминаем, как сокращаются "буквы со степенями":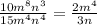 
2.2)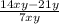 
. Здесь нужно заметить, что в числителе дроби за скобку можно вынести 7y: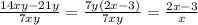 
2.3)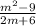
. Важно помнить формулу сокращенного умножения и применить ее в числителе: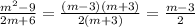 
2.4)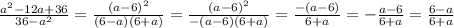
. Здесь в числителе надо наоборот сложить формулу сокращенного умножения, а в знаменателе разложить.
пока что все, а то очень много заданий за )
Истоки алгебры уходят к временам глубокой древности. Арифметические действия над натуральными числами и дробями — простейшие алгебраические операции — встречаются в ранних математических текстах[3]. Ещё в 1650 году до н. э. египетские писцы могли решать отвлечённые уравнения первой степени и простейшие уравнения второй степени, к ним относятся задачи 26 и 33 из папируса Ринда и задача 6 из Московского папируса (так называемые задачи на «аха»). Предполагается, что решение задач было основано на правиле ложного положения[9]. Это же правило, правда, крайне редко, использовали вавилоняне[10].
Вавилонские математики умели решать квадратные уравнения. Они имели дело только с положительными коэффициентами и корнями уравнения, так как не знали отрицательных чисел. По разным реконструкциям в Вавилоне знали либо правило для квадрата суммы, либо правило для произведения суммы и разности, вместе с тем метод вычисления корня полностью соответствует современной формуле. Встречаются и уравнения третьей степени[11]. Кроме того, в Вавилоне была введена особая терминология, использовались шумерские клинописные знаки для обозначения первого неизвестного («длины»), второго неизвестного («ширины»), третьего неизвестного («глубины»), а также различных производных величин («поля» как произведения «длины» и «ширины», «объёма» как произведения «длины», «ширины» и «глубины»), которые можно считать математическими символами, так как в обычной речи уже использовался аккадский язык. Несмотря на явное геометрическое происхождение задач и терминов, использовались они отвлечённо, в частности, «площадь» и «длина» считались однородными[10]. Для решения квадратных уравнений было необходимо уметь осуществлять различные тождественные алгебраические преобразования, оперировать неизвестными величинами. Таким образом был выделен целый класс задач, для решения которых необходимо пользоваться алгебраическими приёмами[11].
После того как была открыта несоизмеримость стороны и диагонали квадрата, греческая математика переживала кризис, разрешению которого выбор геометрии как основы математики и определение алгебраических операций для геометрических величин. Геометрической алгебре посвящена вторая книга «Начал» Евклида, работы Архимеда и Аполлония. С использованием отрезков, прямоугольников и параллелепипедов были определены сложение и вычитание, произведение (построенный на двух отрезках прямоугольник). Такое представление позволило доказать дистрибутивный закон умножения относительно сложения, тождество для квадрата суммы. Алгебра первоначально была основана на планиметрии и при в первую очередь для решения квадратных уравнений[12]. Вместе с тем к алгебраическим уравнениям сводятся сформулированные пифагорейцами задачи об удвоении куба и трисекции угла, построение правильных многоугольников[13]. Решение кубических уравнений получило своё развитие в работах Архимеда (сочинения «О шаре и цилиндре» и «О коноидах и сфероидах»), который исследовал в общем виде уравнение {\displaystyle x^{3}+ax+b=0}x^{3}+ax+b=0. Отдельные задачи решались с конических сечений[14].
Неожиданный переход к алгебре, основанной на арифметике, произошёл в работах Диофанта, который ввёл буквенные обозначения: неизвестное число он назвал «число», вторую степень неизвестного — «квадрат», третью — «куб», четвёртую — «квадрато-квадрат», пятую — «квадрато-куб», шестую — «кубо-куб». Также он ввёл обозначения для отрицательных степеней, свободного члена, отрицательного числа (или вычитания) и знака равенства. Диофант знал и использовал правило переноса вычитаемого из одной части уравнения в другую и правило сокращения равных членов[15]. Исследуя уравнения третьей и четвёртой степеней, Диофант для нахождения рациональной точки на кривой использует такие методы геометрической алгебры, как провести касательную в рациональной точке кривой или провести прямую через две рациональные точки. В X веке «Арифметика» Диофанта, в которой он изложил свои методы, была переведена на арабский язык, а в XVI веке достигла Западной Европы, оказав влияние на работы Ферма и Виета. Идеи Диофанта можно заметить также в работах Эйлера, Якоби, Пуанкаре и других математиков вплоть до начала XX века. В настоящее время проблемы Диофанта принято относить к алгебраической геометрии[16].
Объяснение:
выбери основное
x ≤ 16
-x ≤ 16
x ≤ 16
x ≥ -16
x ∈ [-16, 16]
ответ : x ∈ [-16, 16]
2) |x| > 10
x > 10
-x > 10
x > 10
x < -10
x ∈ (-∞; -10) ∪ (10; +∞)
ответ : x ∈ (-∞; -10) ∪ (10; +∞)